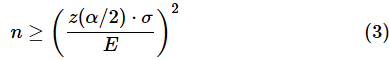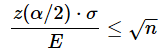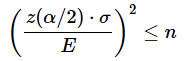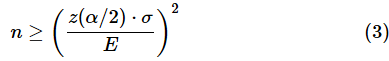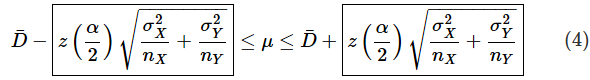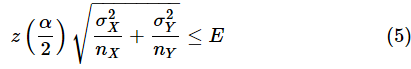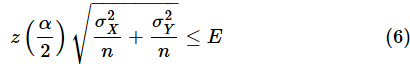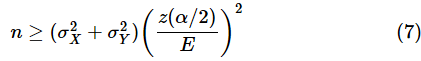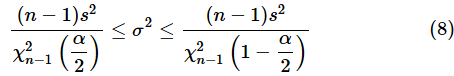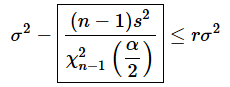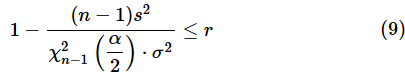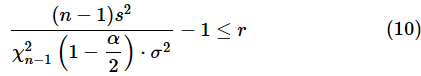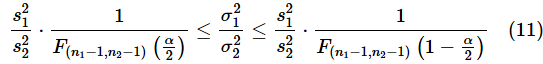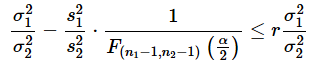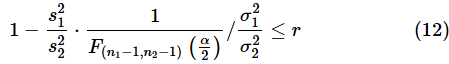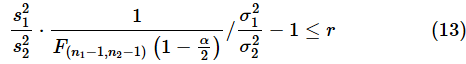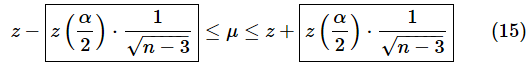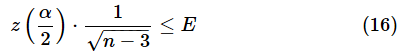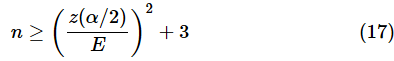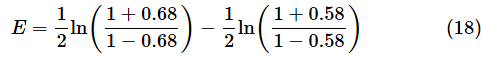[データ分析]区間推定のために必要なサンプルサイズはどれぐらい?:やさしい推測統計(区間推定編)
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載(区間推定編)の第8回。今回は適切に区間推定を行うために必要なサンプルサイズの求め方とその考え方を解説します。
連載:
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」に続く「推測統計(区間推定編)」です。
この連載では、観測されたデータを基に、母集団の母数について区間推定を行う方法を説明します。身近に使える表計算ソフト(Microsoft ExcelやGoogleスプレッドシート)を使いながら具体的に事例を見ていきます。
必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。
筆者紹介: IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。健康のために始めたウォーキングの友として、歩数によって経験値やアイテムが獲得できるゲームを始めるも、自宅でできるバトルに夢中になりすぎてむしろインドア化に拍車がかかった感も。最近、欲しいと思っているものは柔軟な身体と鋼のメンタル。大切だと思っていることは車間距離。
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計(区間推定編)、第8回(番外編)です。前回は正規分布に従う2つの群(グループ)の母相関係数を区間推定しました。しかし、小さなサンプルサイズでは、求められた結果にあまり意味がないというお話もしました。そこで、今回は区間推定を行うのにどの程度のサンプルサイズが必要であるかを求めたいと思います。この連載『やさしい推測統計(区間推定編)』の総まとめとして、平均値の区間推定から相関係数の区間推定まで、全ての場合についてサンプルサイズの見積り方法を見ていきます。
区間推定にはどれぐらいのサンプルサイズが必要か
区間推定に必要なサンプルサイズは、信頼水準αと、許容できる誤差Eによって決められます。この連載の第2回で取り組んだ母平均の区間推定を例に、基本的な考え方を見てみましょう。資格試験の結果を基に、社員全体の平均を区間推定する、という例でした(図1)。
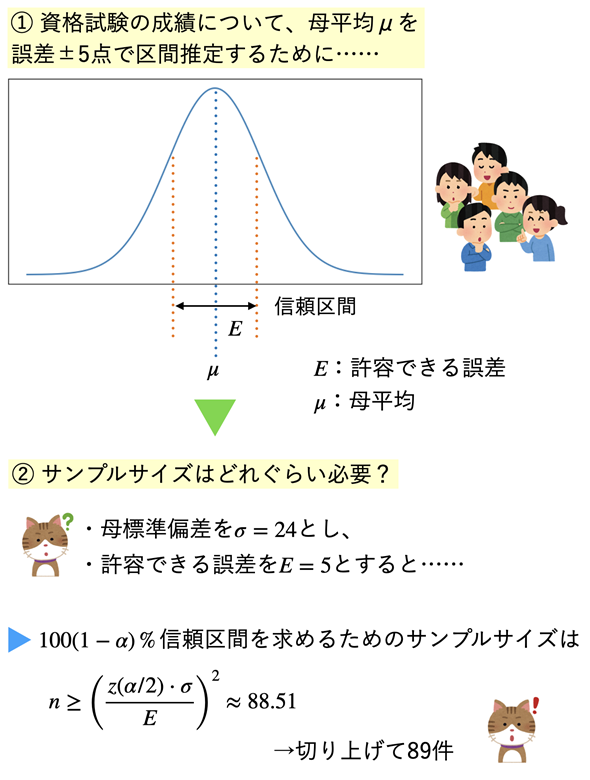 図1 母平均の区間推定に必要なサンプルサイズは幾つ?
図1 母平均の区間推定に必要なサンプルサイズは幾つ?信頼区間の半分が、許容できる誤差E以下になればよい。母標準偏差をσとすると、図の下に書かれた式でサンプルサイズnが求められる。この例であれば、誤差を5点まで許容するなら、89件のサンプルが必要ということになる。
図1の下に記した式は信頼区間の半分の幅が、許容できる誤差E以下になるようにnを逆算したものです。このようにしてnを求めるというのが基本的な考え方です。具体的な計算方法についてはこれから見ていくので、ここでは、nを逆算する、という考え方だけ理解していただければオーケーです。なお、以降「信頼区間の半分の幅」を、信頼区間の半幅と略記することにします。
母平均を区間推定するためのサンプルサイズを求める
母平均の信頼区間は以下の式で求められました(母分散σ2が既知の場合)。
枠で囲んだ部分が信頼区間の半幅です。これが許容できる誤差E以下になればいいので、
という不等式が立てられます。この不等式をnについて解けば、必要なサンプルサイズが求められます。不等式を解く過程は後で見ることとして、結果だけを記すと、
となります。z(α/2)はNORM.S.INV関数で求められるので、早速(3)式に従ってExcelで計算してみましょう。ここでは、σ=24とし、E=5、α=0.05とします。サンプルファイルをこちらからダウンロードし、[サンプルサイズの見積り(母平均)]ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。
図2のようにExcelに入力してください。ここでは操作手順を図のみで示しており、入力内容や計算結果の説明は省略していますので、式(3)と照らし合わせながら、確認してみてください。以降の図も同様のスタイルとなります。図2では、サンプルサイズが89件と、前掲の図1で求めたものと同じ結果になっていることを確認してみてください。
 図2 母平均を区間推定するためのサンプルサイズを求める
図2 母平均を区間推定するためのサンプルサイズを求めるセルE5のNORM.S.INV関数は左側(下側)確率に対する確率変数の値を返すので、右側(上側)のα/2=2.5%点を求めるのであれば、1−α/2=97.5%を指定する必要がある。セルE7は式(3)の右辺の値をそのまま求めたもの。ただし、ROUNDUP関数で小数点以下を切り上げている。
母分散(母標準偏差)が未知の場合はどうすればいい?
図2で見た計算方法は簡単でしたね。ところで、サンプルサイズnを求めるための(3)式には、母標準偏差σが含まれています。しかし、普通、母標準偏差は分かりません。そのような場合には、サンプルから求めた不偏標準偏差を使えばいい……と言いたいところですが、この段階ではまだサンプルが得られていません。サンプルを得るためにサンプルサイズを計算しているのですから。
では、どうすればいいでしょう。そのような場合には、以下のような方法を使います。
- 予備調査として、幾つかのサンプルを取り出し、その不偏標準偏差を使う
- その分野で経験的に得られている標準偏差があれば、その値(あるいは余裕を見てそれよりも大きい値)を使う
- 常識的に考えられる最大値と最小値の差を4で割った値を使う
最小値と最大値の差を4で割った値を使うというのは、正規分布ではμ±2σの範囲に全体の95.45%が含まれることから得られた経験則です。
ちなみに、図1や図2で使ったσ=24という値は、第2回のサンプルデータ(n=10)を基に求めた不偏標準偏差s=23.16(=第2回の図3にある不偏分散s2=536.54のルート)を切り上げたものです。
ところで、母分散(母標準偏差)が分からないときには、標準正規分布ではなくt分布を使うのではないか、という疑問を抱いた方もおられるのではないでしょうか。確かに、厳密にはt分布を使うべきです。しかし、サンプルサイズnが大きければ(一般にn≥ 30であれば)、t分布は標準正規分布で近似できます。そもそも、ある程度大きなサンプルサイズを求めることを想定しているので、(計算が楽な)標準正規分布で代用できるというわけです。
では、次にサンプルサイズnを求めるための(3)式がどのようにして得られたのかを見ていきます。数式が苦手な方は軽くスルーしてもらってもけっこうです。
母平均の区間推定に必要なサンプルサイズの求め方
信頼区間の半幅から必要なnを求める過程を追いかけてみます。(2)式を(3)式に変形するだけです。(2)式は信頼区間の半幅を、許容できる誤差E以下とする、という式でした。分数が幾つか登場して見づらくなるので、
と表します。
両辺に√nを掛けます。
両辺をEで割ります。
両辺を二乗しましょう。
nが左辺になるように、左辺と右辺を入れ替えると、(3)式が得られます。
母平均の差の区間推定に必要なサンプルサイズの求め方
母平均の差の区間推定は、この連載の第5回で解説しました。例えば、対応のないデータで母分散が既知の場合、信頼区間を求めるための式は以下の通りでした。母平均の差μX − μYをμと表しています。nX,nYはそれぞれのサンプルサイズです。
はサンプルから求めた平均の差ですが、ここでは使いません。枠で囲んだ信頼区間の半幅が、許容できる誤差E以下になればいいので、
という不等式が立てられます。ここから、nXとnYを逆算すれば、必要なサンプルサイズが求められるというわけです。ただし、nXとnYが異なると答えが求められません。そこで、データを収集するに当たっての前提としてサンプルサイズnX,nYは等しいものとしましょう。つまり、nX=nY=nとします。すると、(5)式は、
となります。これをnについて解けば以下のようになります。
nXとnYが異なると想定される場合、例えば、Y群がX群に比べて、サンプルがあまり多く取れないと予想される場合は、nX=n, nY=(1/k)nと置き、nYがnXの1/k倍であるものとすれば、(5)式をnについて解くことができます。当然のことながら、実際に区間推定を行う場合には、想定したnの値ではなく、実際に得られたサンプルサイズを使います。
なお、(7)式には、母分散の値σX2, σY2が含まれています。母分散が未知の場合は、上で解説したような方法(予備調査を行って、その不偏分散を使うなど)で計算します。
サンプルファイルの[サンプルサイズの見積り(母平均の差)]ワークシートを開いて試してみてください(図3)。
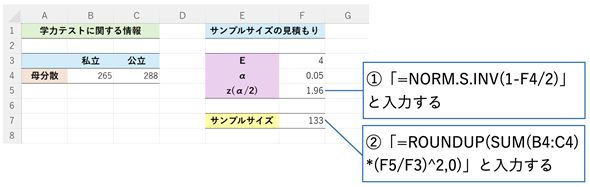 図3 母平均の差を区間推定するためのサンプルサイズを求める
図3 母平均の差を区間推定するためのサンプルサイズを求める学力テストの例で、私立中学の分散を265、公立中学の分散を288としたとき、誤差Eを4以下にしたい場合のサンプルサイズnを求める。セルF7の式は(7)式の右辺の値をそのまま求めたもの。ただし、ROUNDUP関数で小数点以下を切り上げている。
対応のあるデータの場合のサンプルサイズは?
対応のあるデータで平均値の差の区間推定を行う場合は、各サンプルの差を求めて、その母平均を区間推定します。詳しくはこの連載の第5回を参照していただければいいかと思いますが、要するに、2群の平均の差の区間推定ではなく、差の平均の区間推定であるということです。
従って、適切なサンプルサイズを求める方法は、母平均の区間推定の場合と同じ方法を使います。図2で見た[サンプルサイズの見積り(母平均)]ワークシートで、母標準偏差の値(セルB3)に、2群の差の母標準偏差または想定される標準偏差を入力するだけです。
母分散の区間推定に必要なサンプルサイズを求める
どんどん行きましょう。この連載の第3回で見たように、母平均が未知である場合、母分散の信頼区間は以下の式で求められます。
母分散の区間推定の場合、決まった値E以下まで誤差を許容するかどうかという方法よりも、母分散に対して何%以内までの誤差を許容するかどうかという方法がよく使われているようです。許容できる誤差の割合をrと表すと、許容できる誤差の下限は、
となります。母分散σ2から信頼区間の下限(枠で囲んだ部分)までが、母分散のr倍以下である、ということです。両辺をσ2で割れば、
という式が得られます。この式をnについて解けばよさそうですが、そう簡単にはいきません。カイ二乗分布は左右対称な分布ではないので、(9)式が信頼区間の半幅になっていないからです。そこで、許容できる誤差の上限を基に同様の計算を行って、
という式を求めます。簡易な方法としては、(9)式と(10)式の中間(平均)を求めてそれを信頼区間の半幅とすることもできますが、余裕を持ってサンプルサイズnを見積もるなら、(9)式と(10)式の大きい方を信頼区間の半幅とした方がいいでしょう。
というわけで、(9)式と(10)式からnの値を逆算したいのですが、ちょっと困ったことがあります。カイ二乗分布の自由度としてn−1が指定されており、簡単にはnを逆算できないからです。そういう場合はパソコンの力を借りましょう。nの値を順に変えていき、rが許容できる範囲に入ったときのnの値を適切なサンプルサイズとします。つまり、シミュレーションを行うわけです。
実際のところ、サンプルを取得する前はs2の値は分かりません。また、σ2についても一般には未知です。しかし、nがある程度大きくなると、s2がσ2に近づくので、s2=σ2と仮定できます。すると(9)式と(10)式のs2とσ2が約分できるので、式が簡単になります(以下のサンプルファイルでもs2=σ2と仮定していますが、(9)式と(10)式をそのまま使って計算しています)。
では、サンプルファイルの[サンプルサイズの見積り(母分散)]ワークシートを開いて試してみてください。ここでは、手順が少し長くなるので、図4の後に箇条書きで記します。
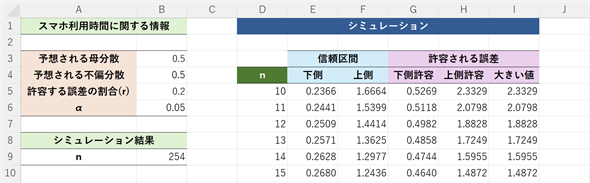 図4 母分散を区間推定するためのサンプルサイズを求める
図4 母分散を区間推定するためのサンプルサイズを求めるD列に10〜1000までの連番を入力し、E列で(8)式の左辺(信頼区間の下限)、F列で(8)式の右辺(信頼区間の上限)を求めている。G列は(9)式の左辺、H列は(10)式の左辺。I列で、G列とH列の大きい方の値を求めている。シミュレーションの結果を基にセルB8にXLOOKUP関数を入力して、I列を検索し、セルB4の「許容する誤差の割合(r)」以下になったときのD列の値を返す。具体的な関数の入力方法は以下の箇条書きを参照。
手順は以下の通りです。Excelでは、数式を入力しているときにセルD5をクリックすれば、スピル機能が適用された範囲D5#が自動的に入力されます。D5:D995と入力する代わりにD5#を使っても構いません。他の箇所についても同様です。なお、以下の手順はExcel 2021以降のバージョンを対象としています。それ以外の環境(旧バージョンのExcelやGoogleスプレッドシートなど)での操作手順については説明を省略していますので、必要に応じて[サンプルサイズの見積もり(母分散・作成例)]ワークシートをご確認ください。
- セルD5に=SEQUENCE(991,1,10,1)と入力する
- セルE5に=(D5:D995-1)*B4/CHISQ.INV.RT(B5/2,D5:D995-1)と入力する
- セルF5に=(D5:D995-1)*B4/CHISQ.INV.RT(1-B5/2,D5:D995-1)と入力する
- セルG5に=1-E5:E995/B3と入力する
- セルH5に=F5:F995/B3-1と入力する
- セルI5に=MAX(G5,H5)と入力して、セルI995までコピーする
- セルI5の右下に表示されているフィルハンドル(小さな四角)をダブルクリックすると、自動的にセルI995までコピーされる
- セルB8に=XLOOKUP(B4,I5:I995,D5:D995,#N/A,-1,1)と入力する
母分散の比の区間推定に必要なサンプルサイズを求める
母分散の比については、この連載の第6回で、母平均が未知の場合の区間推定の方法を紹介しました。式は以下の通りです。
サンプルサイズの求め方は母分散の区間推定の場合と同様です。
に対してr倍の誤差までを許容するなら、許容される誤差の下限は、
となるので、両辺を
で割れば、
という式が得られます。許容される誤差の上限についても同様に、
となります。n1,n2を変えていき、(12)式と(13)式の大きい方が、r以下になるn1,n2を求めるといい、ということです。ただし、n1とn2が異なると、シミュレーションの繰り返し数が増えるので、以下の例ではn1=n2=nとして計算してみます。また、nはある程度の大きさとなるはずなので、s12=σ12,s22=σ22と仮定します。
サンプルファイルの[サンプルサイズの見積り(母分散の比)]ワークシートを開いて試してみてください。手順が少し長くなるので、図5の後に箇条書きで記します。
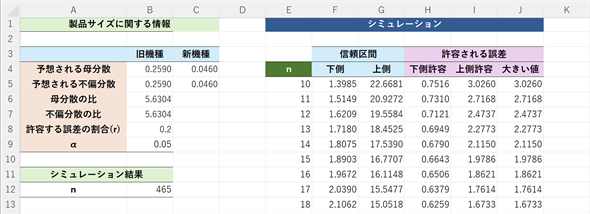 図5 母分散の比を区間推定するためのサンプルサイズを求める
図5 母分散の比を区間推定するためのサンプルサイズを求めるE列に10〜1000までの連番を入力し、F列で(11)式の左辺(信頼区間の下限)、G列で(11)式の右辺(信頼区間の上限)を求めている。H列は(12)式の左辺、I列は(13)式の左辺。J列で、H列とI列の大きい方の値を求めている。シミュレーションの結果を基にセルB12にXLOOKUP関数を入力して、J列を検索し、セルB8の「許容する誤差の割合(r)」以下になったときのE列の値を返す。具体的な関数の入力方法は以下の箇条書きを参照。
手順は以下の通りです。ExcelではE5:E995の代わりにE5#と入力しても構いません。他の箇所についても同様です。なお、以下の手順はExcel 2021以降のバージョンを対象としています。それ以外の環境の方は、必要に応じて[サンプルサイズの見積もり(母分散の比・作成例)]ワークシートをご確認ください。
- セルB6に=B4/C4と入力する
- セルB7に=B5/C5と入力する
- セルE5に=SEQUENCE(991,1,10,1)と入力する
- セルF5に=B7/F.INV.RT(B9/2,E5:E995-1,E5:E995-1)と入力する
- セルG5に=B7/F.INV.RT(1-B9/2,E5:E995-1,E5:E995-1)と入力する
- セルH5に=1-F5:F995/B6と入力する
- セルI5に=F5:F995/B3-1と入力する
- セルJ5に=G5:G995/B6-1と入力して、セルI995までコピーする
- セルJ5の右下に表示されているフィルハンドル(小さな四角)をダブルクリックすると、自動的にセルJ995までコピーされる
- セルB12に=XLOOKUP(B8,J5:J995,E5:E995,#N/A,-1,1)と入力する
母相関係数の区間推定に必要なサンプルサイズを求める
母相関係数の区間推定について、相関係数の分布には偏りがあるのでフィッシャー変換を行う必要があるというお話を前回しました。適切なサンプルサイズを求める場合も、フィッシャー変換の必要があります。
母相関係数ρをフィッシャー変換すると、以下のようになります。
μの信頼区間は以下の式で求められました。枠で囲んだ部分が信頼区間の半幅です。
信頼区間の半幅を誤差E以下にするということなので、
という不等式が立てられます。(16)式をnについて解くと、
となります。ただし、Eはフィッシャー変換後の値なので、相関係数の誤差を0.1以下とする、ということであれば、誤差をフィッシャー変換して求める必要があります。例えば、想定される母相関係数を0.58とし、0.1以下の誤差(=0.68まで)とするなら、それらをフィッシャー変換して差を求めます(下方向への0.1以下の誤差については後述します)。従って、
となります。これを(17)式に当てはめればいいということです。(18)式の各項はFISHER関数を使って求められるのでEの値は簡単に計算できます(図6)。
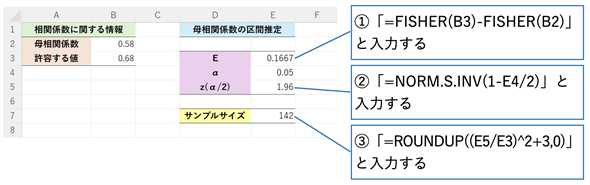 図6 母相関係数を区間推定するためのサンプルサイズを求める
図6 母相関係数を区間推定するためのサンプルサイズを求めるフィッシャー変換はFISHER関数に値を指定するだけなので簡単。セルE3でフィッシャー変換後の誤差を求めている。セルE5でz(α/2)点の値を求め、(17)式に従ってセルE7でnの値を計算すればよい。
n=142という値が得られてメデタシメデタシ、といきたいところなのですが、相関係数の分布は左右対称ではないので、誤差を0.1とするといっても、0.48〜0.58の場合(=図6は0.58から上方向に+0.1していますが、下方向に−0.1した場合)には図6とは異なる結果になってしまいます。その場合も考慮する必要がありますね。セルB3に0.48という値を入力してみてください。セルE7の値は201になるはずです。従って、下方向も考慮するなら、サンプルサイズは余裕を見て201件としておいた方がいいということになります。
今回は、『やさしい推測統計(区間推定編)』の最終回として、適切なサンプルサイズnの求め方を、さまざまな場合について解説しました。
次回からは『やさしい推測統計(仮説検定編)』という新連載に入る予定です(両連載の目次はこちらにまとめています)。仮説検定では、例えば「2群の母平均は等しい」といった仮説が棄却できるか、そうでないかをP値と呼ばれる数値で表します。明確な値が得られるので、白黒付けやすいように思われますが、取り扱いには注意が必要です。計算方法だけでなく、そういった注意点についても連載の中で触れていきたいと思います。
次回からの展開もお楽しみに! なお、新連載として第1回からスタートするため、現在の「次回の掲載をメールで受け取る」設定は引き継がれません。ご注意ください。できるだけ早い公開(1〜2カ月後)を目指しますので、@IT Deep Insiderの新着記事や、Xアカウント(@DeepInsiderJP)を定期的にチェックしていただければと思います。
Copyright© Digital Advantage Corp. All Rights Reserved.


 羽山博
羽山博