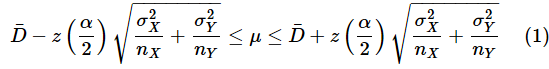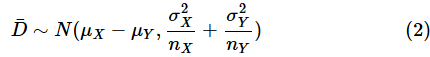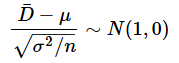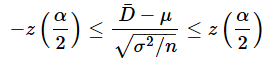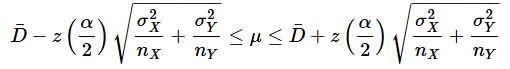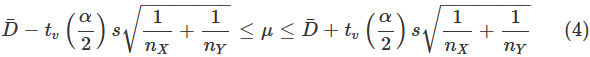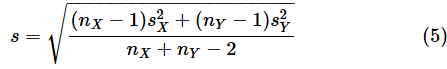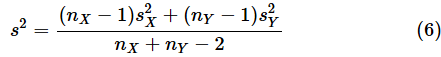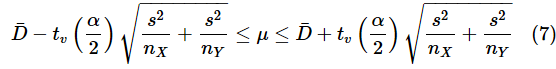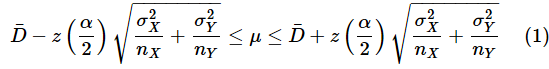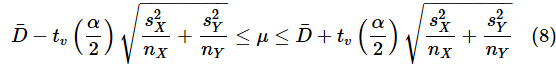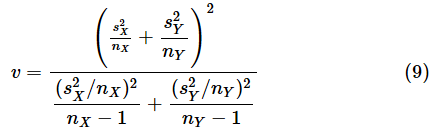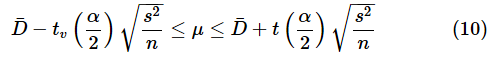[データ分析]母平均の差の区間推定 〜 私立と公立の中学生で学力テストの差はどれぐらい?:やさしい推測統計(区間推定編)
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載(区間推定編)の第5回。今回は正規分布する母集団の平均の差を区間推定する方法と考え方を解説します。
連載:
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」に続く「推測統計(区間推定編)」です。
この連載では、観測されたデータを基に、母集団の母数について区間推定を行う方法を説明します。身近に使える表計算ソフト(Microsoft ExcelやGoogleスプレッドシート)を使いながら具体的に事例を見ていきます。
必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。
筆者紹介: IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。健康のために始めたウォーキングの友として、歩数によって経験値やアイテムが獲得できるゲームを始めるも、自宅でできるバトルに夢中になりすぎてむしろインドア化に拍車がかかった感も。最近、欲しいと思っているものは柔軟な身体と鋼のメンタル。大切だと思っていることは車間距離。
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計(区間推定編)、第5回です。前回は頻度主義での信頼区間とベイズ主義での確信区間の違いについて解説しました。前回までで、区間推定の基本的な考え方については一通り解説したことになります。
今回は応用例として母平均の差を区間推定する方法を解説します。独立した2つの群(グループ)の母分散が既知である場合、未知だが等しいと仮定できる場合、未知で等しいと仮定できない場合など、さまざまな場合があるので、一つずつ具体的な方法を紹介していきます。
今回の手法は、ビジネスの現場(マーケティングでの商品比較など)や医療の分野(治療法や薬の効果の比較)、教育・研究の場面(学力調査や大学での統計研究など)で、「2つのグループに違いがあるか、あるとすればどれくらいか」を知るためによく使われています。このように今回からは、現実の課題に応用しやすい内容となっていきます。実践で活用できるよう、ぜひしっかりと身に付けていきましょう。
母平均の「差」の区間推定とは
前回までは、1つの母集団について、その平均や標準偏差を区間推定する方法を見てきました。今回の例では、2つの独立した正規母集団について、母平均の差を区間推定します(図1)。また、対応のあるデータについても、母平均の差の区間推定を行います。「独立」や「対応のある」の意味については、図1の後で説明します。なお、母集団が正規分布に従っていることが前提ですが、サンプルサイズが大きい場合(一般に30以上と言われています)や極端な分布の偏りがない場合は、母集団が正規分布でなくても母平均の差の区間推定ができます。以下の例では母集団が正規分布しているものとして話を進めます。
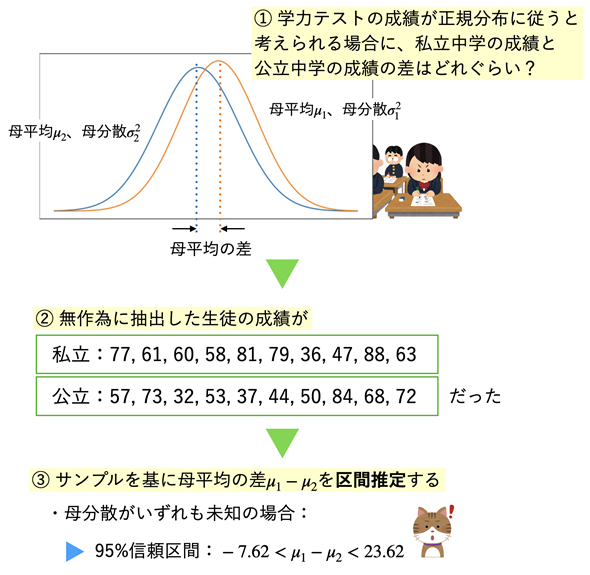 図1 母平均の差を区間推定するための考え方と手順
図1 母平均の差を区間推定するための考え方と手順2つの独立した母集団が正規分布するという前提の下、母集団から取り出されたサンプルを基に母平均の差を区間推定する。この例は、母分散は未知であり、その2つの母分散が等しいとは仮定できない場合と考えられる。母分散が既知の場合や、2つの母分散が等しいと仮定できる場合などに分けて、これから計算の方法を見ていく。
図1の例では、サンプルから得られた平均は、私立が65点、公立が57点なので、平均の差(点推定)は8点です。一方、区間推定では、ある程度の幅を持たせて母平均の差を推定するということでした。上でも少し触れたように、母平均の差を区間推定する場合、
- 母分散が既知の場合
- 母分散は未知だが、2つの母分散が等しいと仮定できる場合
- 母分散が未知の場合(2つの母分散が等しいと仮定できない場合)
に分けて見ていく必要があります。また、「独立した2群の場合」だけでなく、「対応のあるデータの場合」も異なる方法となります。
独立した2群とは、図のような私立中学の生徒と公立中学の生徒のように、それぞれのサンプルが別々の生徒であるようなケースです。先ほど紹介した場合分けは、この「独立した2群」のデータを対象としたものです。
対応のあるデータとは、同じ生徒が第1回の試験を受けた成績と第2回の試験を受けた成績というようなケースです。
図1のデータは架空のデータですが、国立教育政策研究所の「令和6年度全国学力・学習状況調査報告書【中学校/国語】」のデータを参考にしています(クリックするとPDFファイルが開かれます)。公立中学よりも、入試のある私立中学の成績がいいのは(受験のための勉強をするので)当然と言えば当然ですが、学力テストの結果だけで学校の価値が決まるものではもちろんありません。念のため。
信頼区間を求めるための式と計算の具体的な方法を、それぞれの場合に分けて見ていきます。Excelには母平均の差の信頼区間を求めるための関数がないので、掲載した式に従って計算する必要があります。もちろん、不偏分散や不偏標準偏差、t分布のα/2点などを求めるためにExcelの関数が使えるので、実際にやってみるとそれほど難しくはありません。
ただし、今回は私立中学と公立中学という2つの群があるので、利用する文字も多くなります。これまで一般的に使ってきた文字と違いはありませんが、どちらの群であるかを添え字(XとY)で区別して整理しておきます(表1)。なお、サンプルから求められる値については「*」を付け、図1での値も示しておきます。
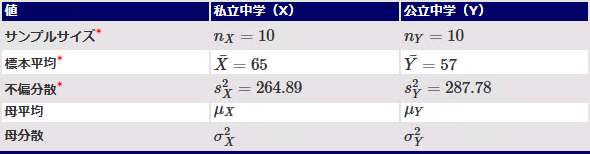 表1 今回使う変数の一覧
表1 今回使う変数の一覧標本平均や母平均などを一般的に表す文字を使うが、添え字でどちらの群であるかを区別する。どの文字が何を表しているか迷ったときには、この表を参照するとよい。ちなみに、サンプルサイズ、標本平均、不偏分散は変数だが、母平均と母分散は定数と考えられる。
今回は、母平均の差の信頼区間を求めるので、「差」を表す値についても文字で表しておきます。
母平均の差を区間推定してみよう(母分散が既知の場合)
ここからは信頼区間を求めるための式を示した後、Excelを使って計算してみます。式の意味(定義)が分かれば、それに従って計算するのは簡単です。
まず、2つの独立した母集団について、母分散が既知の場合に母平均の差を区間推定します。母分散が既知であるというのは実際には考えにくいので、かなり無理がありますが、図1の例で、私立中学の母分散σX2が265、公立中学の母分散がσY2が288であるものとして計算してみましょう。
母分散が既知の場合、母平均の差の信頼区間は以下の式で求められます(式の詳しい意味については後のコラムで解説します)。z(α/2)は標準正規分布のα/2点の値なので、NORM.S.INV関数で求められます。
サンプルファイルをこちらからダウンロードし、[母平均の差の区間推定 (母分散が既知)]ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。操作方法は図2の後に箇条書きで記します。
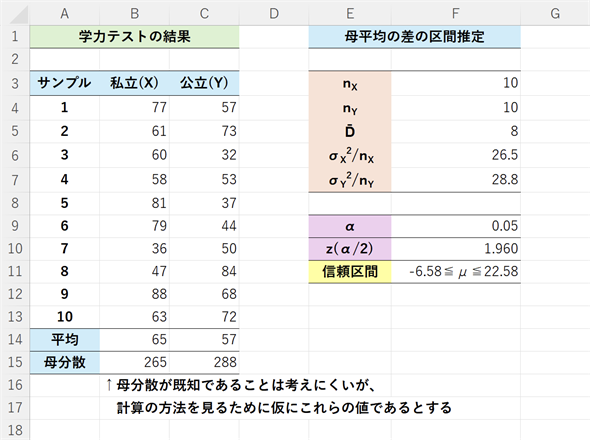 図2 母平均の差の信頼区間を求める(母分散が既知の場合)
図2 母平均の差の信頼区間を求める(母分散が既知の場合)NORM.S.INV関数にα/2の値を指定すると、左側確率に対する値(負の値)が求められる。標準正規分布は左右対称な分布なので、絶対値を求めれば右側確率に対するz(α/2)点の値が求められる。具体的な操作については、以下の箇条書きを参照。
手順は以下の通りです。
- セルB14に=AVERAGE(B4:B13)と入力する
- セルC14に=AVERAGE(C4:C13)と入力する
- セルF3に=COUNT(B4:B13)と入力する
- セルF4に=COUNT(C4:C13)と入力する
- セルF5に=B14-C14と入力する
- セルF6に=B15/F3と入力する
- セルF7に=C15/F4と入力する
- セルF10に=ABS(NORM.S.INV(F9/2))と入力する
- セルF11に=TEXT(F5-F10*SQRT(F6+F7),"0.00")&"≦μ≦"&TEXT(F5+F10*SQRT(F6+F7),"0.00")と入力する
結果は、−6.58 ≤ μ ≤ 22.58となりました。私立中学と公立中学の平均点の差について、サンプルを基に95%信頼区間を求めると-6.58〜22.58となったというわけです。
点推定では8点の差があるという結果でしたが、区間推定ではかなりの幅があるように思われます。これは、サンプルサイズが10と小さいためです。(1)式を見ると、n1やn2の値が大きくなると、ルートの中の部分が小さくなるので、信頼区間が狭くなることが分かると思います。
コラム 母平均の差の信頼区間はどのように計算されるか
ここからは、(1)式がどのようにして導き出されたかをお話しします。単に確率変数がどのような分布に従うかが分かれば、これまでの連載で見てきたのと同じ考え方で信頼区間が求められます。
2つの独立した正規母集団N(μX,σX2)とN(μY,σY2)から、幾つかのサンプルを取り出し、
を求めることを何度も繰り返すと、
は、中心極限定理により、以下のような正規分布に従います。
このことはシミュレーションで確かめることができます。ただし、話が本題からそれてしまうので、これ以上は解説しません。サンプルファイルの最後にある[平均の差の分布]ワークシートにシミュレーションの例を含めておくので、興味のある方はご参照ください。また、こちらにPythonでのサンプルプログラムを掲載しておきます。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます(Googleアカウントでのログインが必要です)。最初のコードセルをクリックし、[Shift]+[Enter]キーを押してPythonのコードを実行してみてください。
(2)式に戻りましょう。式を簡単にするために
と置くと、以下のようになります。
これを標準化して、平均が0に、分散が1になるように調整します。……というのは、この連載の第2回でやったのと全く同じ手順です。
これが、−z(α/2)〜z(α/2)の範囲に入るということなので、
という不等式が立てられます。これをμについて解くと、
となります。σ2/nを元に戻しましょう。(3)式の右辺を代入すればいいですね。
となり、(1)式が導き出されました。
母平均の差を区間推定してみよう(母分散が未知だが等しいと仮定できる場合)
上で見てきた「母分散が既知の場合」というのは、実際には考えにくい状況です。では、母分散は未知だが、2つの母集団で等しいと仮定できる場合はどうでしょうか。やはり、このような状況もあまり考えにくいですね。ですが、順を追って見ていくために、そのような場合の計算方法についても見ておきましょう。まず、信頼区間を求めるための式を掲載します。以下の式の意味については後述します。
ただし、tv(α/2)は自由度v=nX+nY−2のt分布のα/2点で、
です。
図1の例でも、私立中学の生徒と公立中学の生徒では成績のばらつきが異なるかもしれないので、等分散であるという前提で分析することは適切ではありません。しかし、ここでは、計算の手順を見るために、あえて同じ例でやってみましょう。
等分散であるかどうかを確認するために、事前に等分散性の検定を行うことも考えられます。ただし、仮定の上に仮定を重ねることになり、適切な結果が得られないことがあるので、実際には次の項で説明する「母分散が未知の場合」の方法を使うのが妥当です。なお、等分散の検定については、この連載の続編(仮説検定編)でお話しする予定ですが、結論だけ言うと「私立中学と公立中学の分散に違いがあるとは言えない」という結果になります(ただし、等しいとは言い切れません)。
母分散が未知の場合にt分布を利用するというのは、この連載の第2回で見た「母平均の区間推定(母平均が未知の場合)」と同じです。(4)式と(5)式を使った計算はかなり面倒ですが、ステップを分けて丁寧に計算していけば、難しくはありません。
では、Excelで計算してみます。サンプルファイルの[母平均の差の区間推定 (等分散)]ワークシートを開いて試してみてください。操作方法は図3の後に箇条書きで記します。
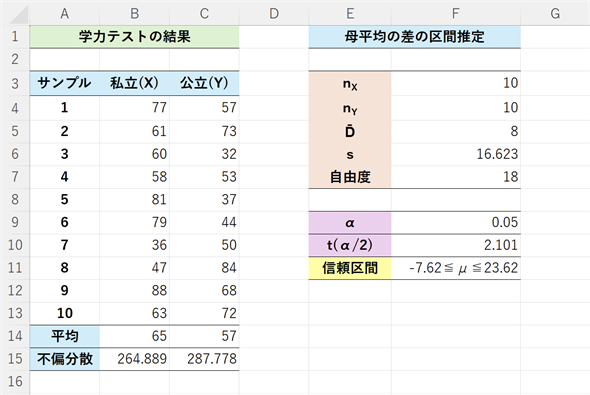 図3 母平均の差の信頼区間を求める(母分散が未知だが等分散の場合)
図3 母平均の差の信頼区間を求める(母分散が未知だが等分散の場合)母分散が未知だが等分散が仮定される場合はサンプルから求めた不偏分散の加重平均を代わりに使い、t分布のα/2点を求める。T.INV.2T関数には両側確率を指定するので、αの値をそのまま指定すればよい。具体的な操作については、以下の箇条書きを参照。
手順は以下の通りです。
- セルB14に=AVERAGE(B4:B13)と入力する
- セルC14に=AVERAGE(C4:C13)と入力する
- セルB15に=VAR.S(B4:B13)と入力する
- セルC15に=VAR.S(C4:C13)と入力する
- セルF3に=COUNT(B4:B13)と入力する
- セルF4に=COUNT(C4:C13)と入力する
- セルF5に=B14-C14と入力する
- セルF6に=SQRT(((F3-1)*B15+(F4-1)*C15)/(F3+F4-2))と入力する
- セルF7に=F3+F4-2と入力する
- セルF10に=T.INV.2T(F9,F7)と入力する
- セルF11に=TEXT(F5-F10*F6*SQRT(1/F3+1/F4),"0.00")&"≦μ≦"&TEXT(F5+F10*F6*SQRT(1/F3+1/F4),"0.00")と入力する
結果は、−7.62 ≤ μ ≤ 23.62となりました。つまり、私立中学と公立中学の平均点の差について、サンプルを基に95%信頼区間を求めると-7.62〜23.62となったことを意味します。
ここで、(4)式と(5)式の意味について補足しておきます。(5)式は、Xの分散とYの分散をそれぞれの自由度で重み付けて平均したもののルート(√)です。ルートを外して分散s2の形にするなら、
となり、加重平均であることが分かりますね。ここで、(4)式のsをルートの中に入れると、
となります。母分散が既知の場合に使った(1)式は
だったので、対比して見ると、σ2と標準正規分布の代わりにs2とt分布を使っていることがよく分かります。
母平均の差を区間推定してみよう(母分散が未知の場合)
続いて、母分散が未知で、2つの母集団が等分散と仮定できない場合(単に「母分散が未知の場合」と呼びます)です。ようやく、現実的によくある例になりました。図1の例もこの場合に当てはまります。これまでと同様に、信頼区間を求めるための式を掲載しておきます。
ただし、tv(α/2)は自由度vのt分布のα/2点で、
です。(8)式は(7)式と同じですね。母分散が等しいと仮定できないので、それぞれの不偏分散を使っているだけです。(9)式では自由度を調整しています。ただし、導出はかなり複雑な過程になるので、ここでは省略します。
(9)式で求めた自由度は整数にならないので、小数点以下は切り捨て、または切り上げて使うのが一般的です。小数点以下を切り捨てて自由度を小さくすると、信頼区間は狭くなります。逆に切り上げると信頼区間は広くなります。余裕を持って信頼区間を求めるには、切り上げた方がいいのですが、平均値の差の検定では、切り捨てた方が厳しい判定ができます(平均値の差の検定については、仮説検定編でお話しします)。なお、ExcelのT.INV.2T関数では小数点以下のある自由度を指定すると、自動的に小数部が切り捨てられた値が使われ、科学技術向けのアルゴリズムや関数をPythonで利用するためのライブラリであるSciPyが提供するscipy.stats.tクラスのppf関数では小数点以下のある自由度がそのまま使われます。
Excelで計算してみましょう。サンプルファイルの[母平均の差の区間推定 (母分散が未知)]ワークシートを開いて試してみてください。操作方法は図4の後に箇条書きで記します。
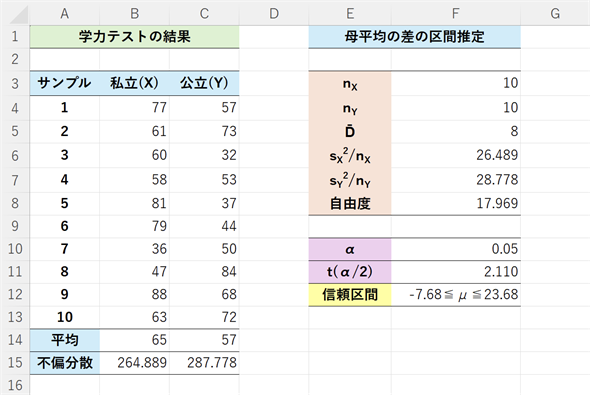 図4 母平均の差の信頼区間を求める(母分散が未知の場合)
図4 母平均の差の信頼区間を求める(母分散が未知の場合)母分散が未知で等分散が仮定できない場合、それぞれのサンプルから求めた不偏分散を代わりに使う。ただし、自由度の調整が必要になる。具体的な操作については、以下の箇条書きを参照。
手順は以下の通りです。
- セルB14に=AVERAGE(B4:B13)と入力する
- セルC14に=AVERAGE(C4:C13)と入力する
- セルB15に=VAR.S(B4:B13)と入力する
- セルC15に=VAR.S(C4:C13)と入力する
- セルF3に=COUNT(B4:B13)と入力する
- セルF4に=COUNT(C4:C13)と入力する
- セルF5に=B14-C14と入力する
- セルF6に=B15/F3と入力する
- セルF7に=C15/F4と入力する
- セルF8に=(F6+F7)^2/(F6^2/(F3-1)+F7^2/(F4-1))と入力する
- セルF11に=T.INV.2T(F10,F8)と入力する
- セルF12に=TEXT(F5-F11*SQRT(F6+F7),"0.00")&"≦μ≦"&TEXT(F5+F11*SQRT(F6+F7),"0.00")と入力する
結果は、−7.68 ≤ μ ≤ 23.68となりました。つまり、私立中学と公立中学の平均点の差について、サンプルを基に95%信頼区間を求めると-7.68〜23.68になったということです。
やはり、かなりの幅があります。サンプル数が少ないこともあって、これだけで私立中学の平均点の方が高いと判断するのは性急かもしれません。
実は、平均値の差の検定を行うと「私立中学の平均点の方が高いとは言えない」という結果になります。毎回もったいぶるようで申し訳ないのですが、平均値の差の検定については、この連載の続編(仮説検定編)でお話しする予定です。
母平均の差を区間推定してみよう(対応のあるデータの場合)
対応のあるデータとは、同じ人が試験を2回受けた場合の各回の成績のようなデータです。具体例はすぐ後で見ることとして、平均の差の信頼区間を求める式を掲載しておきます。
ただし、tv(α/2)は自由度v=n−1のt分布のα/2点で、s2はD=X−Yの不偏分散です。
この場合は、各データの差をサンプルとして平均の区間推定を行うだけです。学力テストの例で言えば、1回目の母平均と2回目の母平均の差(μX−μY)について区間推定をするのではなく、1回目と2回目の差の母平均(μX−Y)について区間推定をするということです。
といっても、実感が湧きませんね。具体例で見るのが分かりやすいでしょう。Excelで計算してみます。サンプルファイルの[母平均の差の区間推定 (対応のあるデータ)]ワークシートを開いて試してみてください。
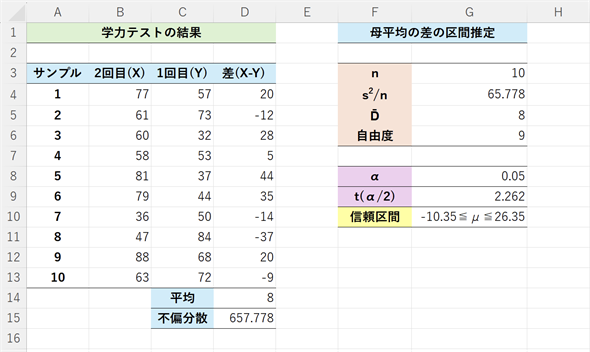
図5のデータは、同じ人がテストを2回受けた例になっています。例えばサンプル1の人は、1回目の成績が57点、2回目の成績が77点だったという具合です。表では2回目の成績が左の列になっていますが、単にこれまでの例と同じようにX−Yが正になるようにするためです。(10)式に従って計算する手順を図の後に示しておきます。
- セルD4に=B4:B13-C4:C13と入力する(スピル機能によりセルD13までが一気に求められる)
- スピル機能が使えない場合は、あらかじめセルD4〜D13を選択しておき、セルD4に=B4:B13-C4:C13と入力して、入力終了時に[Ctrl]+[Shift]+[Enter]キーを押す(配列数式として入力される)
- Google スプレッドシートの場合は=ARRAYFORMULA(B4:B13-C4:C13)と入力する
- セルD14に=AVERAGE(D4:D13)と入力する
- セルD15に=VAR.S(D4:D13)と入力する
- セルG3に=COUNT(A4:A13)と入力する
- セルG4に=D15/G3と入力する
- セルG5に=D14と入力する
- セルG6に=G3-1と入力する
- セルG9に=T.INV.2T(G8,G6)と入力する
- セルG10に=TEXT(G5-G9*SQRT(G4),"0.00")&"≦μ≦"&TEXT(G5+G9*SQRT(G4),"0.00")と入力する
結果は、−10.35 ≤ μ ≤ 26.35となりました。つまり、学力テスト1回目と2回目の平均点の差について、サンプルを基に95%信頼区間を求めると-10.35〜26.35となったということです。
点推定では1回目から2回目のテストで成績が8点上がっていますが、信頼区間にはかなりの幅がありますね。一概に、2回目の成績が上がったとは言いにくいようです(仮に成績が上がったとしても、学力が上がったのか、テストが簡単だったのかは分かりません)。
今回は、母平均の差について区間推定を行いました。母集団が正規分布すると考えられる独立した2つの群を比較するためには、母分散が既知か未知か、等分散であるかといったことを確認しておく必要があります。また、対応のあるデータの場合は差をサンプルと見なして差の母平均の区間推定を行うということでした。区間推定を行うためには、このような違いを確認した上で、適切な方法を選ぶ必要があるというわけです。
さて、次回は2群の分散の比について区間推定を行います。次回もお楽しみに!
Copyright© Digital Advantage Corp. All Rights Reserved.


 羽山博
羽山博