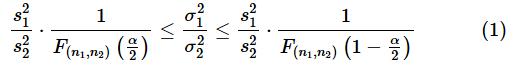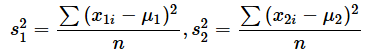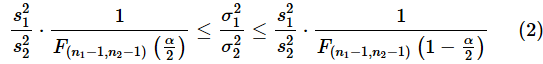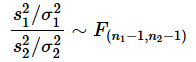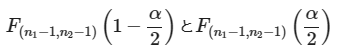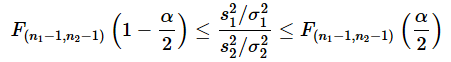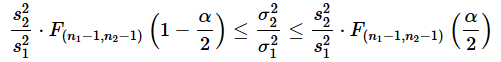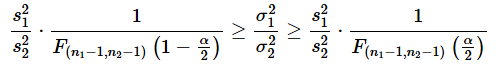［データ分析］母分散の差の区間推定 〜 新機種で製作した製品のばらつきはどの程度が改善されたか？：やさしい推測統計（区間推定編）

連載目次

連載：

『社会人1年生から学ぶ、やさしい推測統計（区間推定編）』

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」に続く「推測統計（区間推定編）」です。
　この連載では、観測されたデータを基に、母集団の母数について区間推定を行う方法を説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。健康のために始めたウォーキングの友として、歩数によって経験値やアイテムが獲得できるゲームを始めるも、自宅でできるバトルに夢中になりすぎてむしろインドア化に拍車がかかった感も。最近、欲しいと思っているものは柔軟な身体と鋼のメンタル。大切だと思っていることは車間距離。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（区間推定編）、第6回です。前回は母平均の差を区間推定する方法について解説しました。今回は母分散の比を区間推定する方法を解説します。正規分布に従う独立した2つの群（グループ）の母平均が既知である場合と未知の場合に分けて具体的な方法を紹介していきます。

　前回の手法は、ビジネスや教育など、さまざまな場面で、2つのグループで成績の差がどの程度あるのか、あるいは、グループ内でどの程度改善されたのかを知るために使われるものでした。今回の手法で分散（＝ばらつき）がどの程度改善されたのかを知ることができれば、製品の品質がより安定したものになったか、といった現実の課題に対応できるようになります。

母分散の「比」の区間推定とは

　前回は、2つの独立した正規母集団について、母平均の「差」を区間推定しました。今回は、母分散の「比」の区間推定です。平均の場合は差を見るのに、分散の場合は、なぜ比なの、という素朴な疑問が湧いてくるかもしれません。

　これに対する答えは、確率分布編の第9回でお話しした通りです。端的に言うと、分散は二乗された値だからです。面積のように二乗された値は、比を取って比較します。よく、東京ドーム何個分という表現を使いますが、その考え方と同じです。東京ドームの面積は約0.047k㎡、2025年4月に開催された大阪・関西万博の会場の面積は1.55k㎡です。ということは、万博会場の広さは1.55/0.047＝32.97、つまり東京ドーム約33個分となりますね。

　図1の例は、母集団が正規分布しているものとして、ある工作機械で加工した製品のサイズに関して、分散の比を区間推定したものです。つまり、旧機種を使用してその製品を加工した場合よりも、新機種を使用して加工した場合の分散がどの程度改善されているのかを知りたい、というわけです。

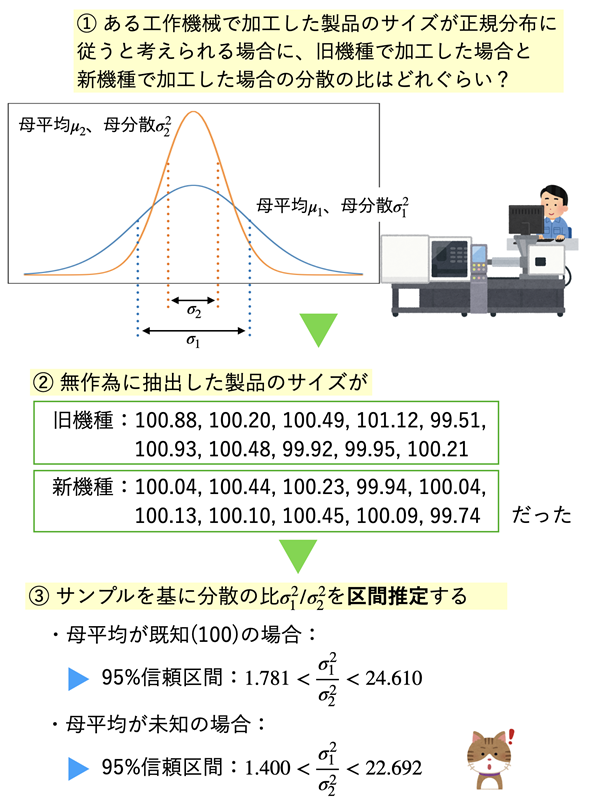図1　母平均の差を区間推定するための考え方と手順
2つの独立した母集団が正規分布するという前提の下、母集団から取り出されたサンプルを基に母分散の比を区間推定する。母平均が既知の場合と未知の場合に分けて、これから計算の方法を見ていく。なお、これらのデータは架空のデータ。

　図1の例では、サンプルから得られた不偏分散は（図中には掲載していませんが）旧機種が0.2595、新機種が0.0460なので、比（旧／新）は5.636です。σ₁²>σ₂²なら、分散の比は1より大きくなり、σ₁²<σ₂²なら、分散の比は1より小さくなるので、この点推定値を見ると、かなり改善されたように思われます。

　では、信頼区間を求めるための式と計算の具体的な方法をそれぞれの場合に分けて見ていきましょう。Excelには母分散の比の信頼区間を求めるための関数がないので、以降に掲載した式に従って計算する必要があります。といっても、不偏分散やF分布のα/2点などを求めるためにExcelの関数が使えるので、実際にやってみるとそれほど難しくはありません。

母分散の比を区間推定してみよう（母平均が既知の場合）

　ここからは信頼区間を求めるための式を示した後、Excelを使って計算してみます。式の意味（定義）が分かれば、それに従って計算するのは簡単です。

　まず、2つの独立した母集団について、母平均が既知の場合に母分散の比を区間推定します。母平均が既知である場合は考えにくいかもしれませんが、例えば、製品の仕様により、サイズが決まった値であると仮定できるような場合です。

　母平均が既知の場合、母分散の比σ₁²/σ₂²の信頼区間は以下の式で求められます（式の詳しい意味については後のコラムで解説します）。

　ただし、

です。

　μ₁は一方の群の母平均、μ₂はもう一方の群の母平均で、x_1iは一方の群の各データ、x_2iはもう一方の群の各データです。s₁²やs₂²は、ExcelのVAR.P関数で求められる分散とは異なることに注意してください。

　ExcelのVAR.P関数では、母平均μ₁やμ₂の代わりに

を使って標本分散s₁²やs₂²の値を求めます。

　F(n₁,n₂)(α/2)は自由度（n₁,n₂）のF分布におけるα/2点の値なので、F.INV.RT関数で求められます。念のためおさらいしておくと、以下の図2に示したF分布の確率密度関数で、オレンジ色のアミカケの部分の面積の合計が全体の5％となり、そのときの右側のF値（図ではxで示してあります）がα/2点、左側のF値が1−α/2点です。

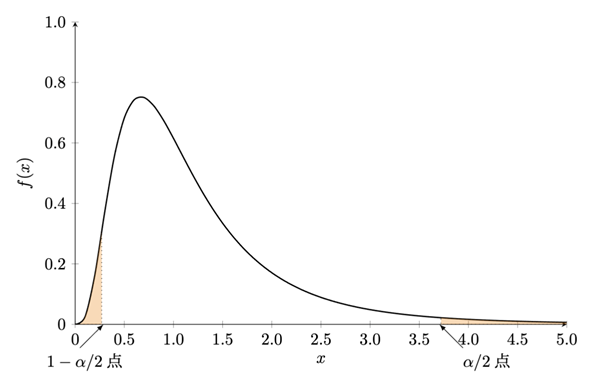図2　F分布のα/2点と1−α/2点
この例は自由度（10,10）のF分布の確率密度関数をグラフ化したもの。α＝0.5の場合、右側（上側）のオレンジ色の部分が全体の面積の2.5％（＝0.025）に当たる。このときのF値がα/2点となる（実際の値は3.7168）。また、左側（下側）のオレンジ色の部分も全体の面積の2.5％。そのときのF値が1−α/2点となる（実際の値は0.2690）。これらの面積を合計すると5％になる。

　分散の比に関する分布としてF分布が使われる理由については、確率分布編の第9回で解説しています。それについては余裕のあるときにまた見ていただくこととして、取りあえず、理屈は抜きにして（1）式で計算してみましょう。

　サンプルファイルをこちらからダウンロードし、［母分散の比の区間推定 (母平均が既知)］ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。操作方法は図3の後に箇条書きで記します。

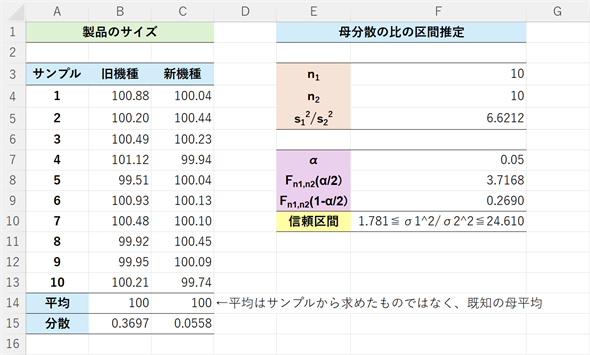図3　母分散の比の信頼区間を求める（母平均が既知の場合）
F.INV.RT関数にα/2の値を指定すると、右側確率に対する値が求められる。左側確率を求めるには、F.INV.RT関数に1−α/2の値を指定する（F.INV関数にα/2の値を指定してもよい）。具体的な操作については、以下の箇条書きを参照。

　手順は以下の通りです。

　セルB15の式ではスピル機能を使い、セルB4〜B13の各データからセルB14の母平均を引いて二乗したものを合計しています。それをセルF3の値（データの個数）で割れば、分散が求められます。セルC15についても同様です。

　セルF10が信頼区間です。数式中では下付き文字やべき乗を表す上付き文字が使えないので、結果が少し見づらくなっていますが、1.781 ≤ σ₁²/σ₂² ≤ 24.610となったことが分かります。旧機種と新機種で加工した製品からサンプルを取り出してサイズを測定し、分散の比の95％信頼区間を求めたところ、1.781〜24.610になったというわけです。比が1より大きいので、新機種でのばらつきが小さくなったと言えそうです（分散の比の検定を行うと「新機種でのばらつきの方が小さい」という結果になります。分散の比の検定については、この連載の続編（仮説検定編）でお話しする予定です）。

母分散の比を区間推定してみよう（母平均が未知の場合）

　母平均が未知の場合についても見てみましょう。こちらの方がありがちな例ですね。母分散の比σ₁²/σ₂²の信頼区間は以下の式で求められます（こちらについても、式の詳しい意味については後のコラムで解説します）。

　ただし、s₁²,s₂²はそれぞれの不偏分散です。

　サンプルファイルの［母分散の比の区間推定 (母平均が未知)］ワークシートを開いて試してみてください。データは同じものを使います。操作方法は図4の後に箇条書きで記します。

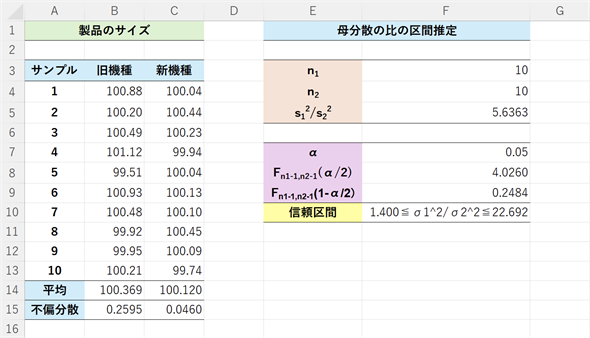図4　母平均の比の信頼区間を求める（母分散が未知だが等分散の場合）
母平均が未知の場合には、サンプルから求めた不偏分散を使い、自由度（n₁−1,n₂−1）のF分布のα/2点と1−α/2点の値を求めて信頼区間を計算すればよい。具体的な操作については、以下の箇条書きを参照。

　手順は以下の通りです。

　結果は、1.400 ≤ σ₁²/σ₂² ≤ 22.692となりました。母平均が未知の場合に旧機種と新機種で加工した製品からサンプルを取り出してサイズを測定し、分散の比の95％信頼区間を求めたところ、1.400〜22.692になったというわけです。

コラム　母分散の比の信頼区間はどのように計算されるか

　最後に、信頼区間を求めるための（1）式や（2）式がどのようにして導き出されたかをお話しします。ここでは、（2）式の方が分かりやすいので、母平均が未知の場合の例でお話しします。

　確率分布編の第9回で解説した通り、2つの正規母集団からサンプルを取り出して求めた不偏分散がs₁²,s₂²であるとすると、s₁²/σ₁²とs₂²/σ₂²の比は、自由度(n₁−1,n₂−2)のF分布に従います。つまり、

と表されます。これが、

の間に入るということなので、

という不等式が立てられます。三辺にs₂²/s₁²を掛けると、

となります。これを逆数にすると、

のように、不等号の向きが逆になります。値を小さい方から並べ替えると、

となり、（2）式と一致します。不偏分散では、母平均の代わりに標本平均を使っているので、独立した情報の個数が1つ減って、自由度が(n₁−1, n₂−1)になっていることに注意してください。この理由については、確率分布編の第8回で解説しましたが、自由度については「この場合はn₁−1, n₂−1になる」のように覚えておいてもらった方が悩まなくて済むかと思います。

　（1）式については、標本分散s₁²,s₂²を求めるために、既知の母平均が使えるので（母平均を求めるために標本の情報を使っていないので）、自由度は(n₁, n₂)となります。

　今回は、母集団が正規分布すると考えられる独立した2つの群について、母分散の比を区間推定する方法を見ました。母平均が既知であるか、未知であるかによって利用する式が異なりますが、手順にそって進めていけば難しくはありませんね。

　次回は相関係数の区間推定を行います。次回もお楽しみに！

「やさしい推測統計（区間推定編）」