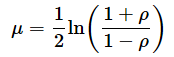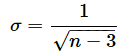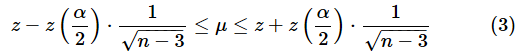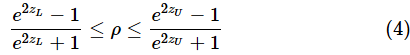［データ分析］相関係数の区間推定 〜 体格指数と糖尿病の進行度の関係はどの程度なのか？：やさしい推測統計（区間推定編）

連載目次

連載：

『社会人1年生から学ぶ、やさしい推測統計（区間推定編）』

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」に続く「推測統計（区間推定編）」です。
　この連載では、観測されたデータを基に、母集団の母数について区間推定を行う方法を説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。健康のために始めたウォーキングの友として、歩数によって経験値やアイテムが獲得できるゲームを始めるも、自宅でできるバトルに夢中になりすぎてむしろインドア化に拍車がかかった感も。最近、欲しいと思っているものは柔軟な身体と鋼のメンタル。大切だと思っていることは車間距離。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（区間推定編）、第7回です。前回は母分散の比を区間推定する方法について解説しました。今回は母相関係数を区間推定する方法を解説します。正規分布に従う2つの群（グループ）の母相関係数をある程度の幅を持たせて推定するための具体的な方法を紹介していきます。

　相関係数は2つのグループの直線的な関係を表す値としてよく知られています。関係の強さが-1〜1の範囲で端的に表されるので、分かりやすいのですが、疑似相関や因果関係との混同などの罠（わな）にはまってしまうこともあります。

　しかし、それ以前に、点推定によって得られたたった1つの値で関係の強さを語ってしまっていいものでしょうか。……というわけで、相関係数についても区間推定をやってみようというのが今回のテーマです。

相関係数の区間推定を行うための考え方と大まかな流れ

　相関係数の区間推定について、図1で大まかな流れを見てみましょう。データはPythonから利用できるscikit-learnのサンプルデータとして引用されている体格指数（BMI）の値と1年後の糖尿病の進行度の例を参考にしたものです。

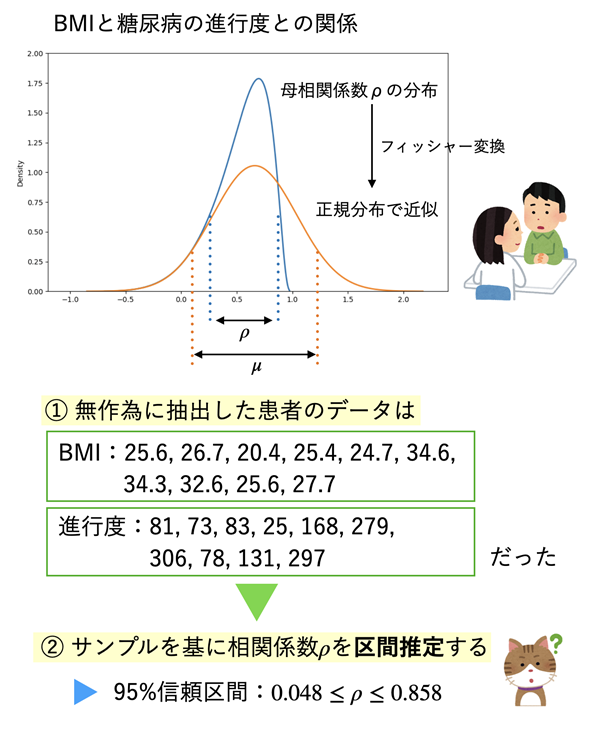図1　母相関係数を区間推定するための考え方と手順
正規分布する2つの母集団について母相関係数の区間推定を行う。相関係数は分布に偏りがあるので、フィッシャー変換（後述）と呼ばれる方法で正規分布に近い形に変換し、信頼区間を求める。その結果をフィッシャー変換の逆変換により元の相関係数の信頼区間とする。図の一番下に示した値は、そのような前提の下、母集団から取り出されたサンプルを基に母相関係数を区間推定した例。

　ここでは、母相関係数をρと表し、サンプルから得られた相関係数をrと表します。ρはギリシア文字で「ロー」と読みます。ラテン文字（いわゆるアルファベット）のrに当たるものです。

　では、母相関係数の区間推定を行うための考え方と手順について、図1で大きな流れを見ていきましょう。多少分からないことがあってもあまり気にせず流れだけ追いかけてください。具体的な計算や操作を見れば実感が湧くと思います。

　まず、図1のグラフの部分をご覧ください。ブルーの曲線（山が高く偏りのある曲線）が相関係数の分布を表すグラフです。ここでは、母相関係数がρ＝0.58となる2つの母集団を想定し、それらの母集団からサンプルを取り出して相関係数を求めたときの、相関係数の分布（確率密度関数）をプロットしてあります。

　相関係数の分布は定義域が-1〜1と限られており、偏りもあります。そこで、フィッシャー変換と呼ばれる方法を利用します。すると、オレンジ色の曲線（ほぼ左右対称になっているグラフ）のような正規分布の形にできます。正規分布であれば、この連載の第3回で見た方法で区間推定ができますね。その信頼区間が図中のμで示した範囲です。具体的な方法は後で説明するので、もう少し流れを見ていきます。

　そのようにして求めた信頼区間をフィッシャー変換の逆変換により、元に戻してあげれば、母相関係数の区間推定ができます。図中のρで示した範囲が、母相関係数の信頼区間だというわけです。

　図1の下半分に示したデータは、実際に10人分のサンプルが得られたとき、それらのサンプルを基に、上記のような考え方に沿って区間推定を行った場合の例です。結果は95％信頼区間が0.048≤ρ≤ 0.858となっています。点推定によって求めた相関係数は、図中には示していませんが0.58です。0.58であれば、相関があるといってよさそうな気がしますが、この例では信頼区間の幅があまりにも広いので、0.58という値はあまりアテにならないことが直感的にも分かります。

母相関係数の区間推定にはフィッシャー変換が必要

　ここまでのお話で、どうやらフィッシャー変換ができれば、相関係数の区間推定ができそうだということが分かったと思います。そこで、フィッシャー変換とフィッシャー変換の逆変換を行うための式を見ておきましょう。

　といっても、以下の式を覚える必要はありません。一応、どのような理屈で計算するのかを追いかけますが、ちょっと難しいかもしれないので、数式が苦手な方は（1）式〜（4）式に沿って計算する、とだけ理解しておいていただいて、Excelでの具体的な計算例に進んでもらってけっこうです（その上で、またここに戻ってくると、理解が進むと思います）。

　フィッシャー変換の式は、

となります。ただし、lnは自然対数です。なお、この式の通りに計算しなくても、ExcelではFISHER関数にrの値を指定するだけでzの値が求められます。

　また、フィッシャー変換の逆変換は、

です。こちらも、ExcelのFISHERINV関数にzの値を指定するだけでrの値が求められます。ハードルがだいぶ下がりましたね。

　例えば、母相関係数ρをフィッシャー変換すると、平均μは、

となり、標準偏差σは

となり、相関係数の分布がN(μ, σ²)で近似できるようになります。この分布の100(1−α)％信頼区間は、

となります。ただし、両辺に単独で登場するzは（1）式のフィッシャー変換で求めたzの値で、

は標準正規分布のα/2点の値です。同じzという文字を使っているのでちょっとややこしいですが、異なるものなので注意してください。なお、

はNORM.S.INV関数で求められます。念のため、（3）式を図解しておきましょう（図2）。

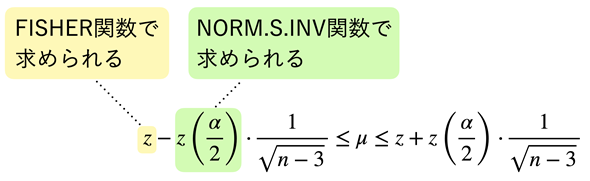図2　フィッシャー変換により正規分布の区間推定を行う
（3）式の左辺だけを図解した。zの値は（1）式で求められる。一方、z(α/2)は標準正規分布のα/2点。同じ文字を使っているが、zは変数で、z()は関数であることに注意。右辺も同様に考えればよい。

　続いて、フィッシャー変換の逆変換を行って元に戻せば、ρの信頼区間が求められます。式が複雑になるので、以下のように、（3）式の左辺をZ_L、右辺をZ_Uと表すことにします（LはLowerの略、UはUpperの略です）。

　フィッシャーの逆変換を行うと以下のような式になります。

　どんどん複雑になるような気がしますが、（4）式の右辺と左辺は、（3）式の右辺と左辺をFISHERINV関数に指定するだけで求められます。こちらも念のために図解しておきます（図3）。

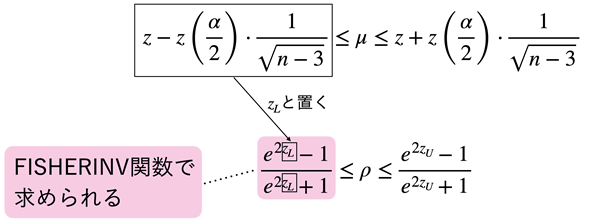図3　フィッシャー変換の逆変換により相関係数の区間推定を行う
（4）式の左辺だけを図解した。式は複雑だが、実際には（3）式で求めた値（枠で囲んだ部分の値）をFISHERINV関数に指定するだけで左辺の値が求められる。右辺も同様に考えればよい。

Excelで母相関係数の信頼区間を求めてみる

　お待たせしました。ExcelのFISHER関数とFISHERINV関数を使って母相関係数の信頼区間を求めてみましょう。データは図1のものを使います。くどいようですが、10件のデータで区間推定をしてもあまり意味がありません。あくまで、計算の方法を理解するために小さなデータで試してみようということです。

　サンプルファイルをこちらからダウンロードし、［母相関係数の区間推定］ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。操作方法は図4の後に箇条書きで記します。

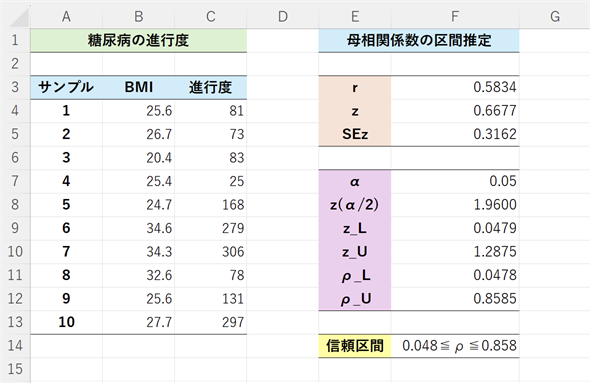図4　母相関係数の信頼区間を求める
FISHER関数にrの値を指定すると、フィッシャー変換を行った結果が求められる。また、FISHERINV関数にzの値を指定するとフィッシャー変換の逆変換を行った結果が求められる。具体的な操作については、以下の箇条書きを参照。

　手順は以下の通りです。（1）〜（4）式の通りに進めていくだけです。

　セルF4でフィッシャー変換を行った値を求めています。セルF5〜F10で正規分布の信頼区間を求め、セルF11とF12でフィッシャー変換の逆変換を行って相関係数の信頼区間を求めている、というわけです。

　なお、標準正規分布のα/2点を求めるセルF8の式は少し注意が必要です。NORM.S.INV関数は左側（下側）の累積確率に対する確率変数の値を返すので、右側（上側）確率に対する確率変数の値を求めるためにはF2/2ではなく、1-F7/2を指定する必要があります。

　セルF14が信頼区間です。10人のサンプルでBMIと糖尿病の進行度の相関係数について95％信頼区間を求めたところ、0.048〜0.858になったというわけです。ほとんど0（無相関）〜ほとんど1（強い正の相関）までの幅なので、これだけでは意味がありませんね。……というわけで、完成例のワークシートにはこのデータを作成するために参考にした元のデータ442件で同じ計算をしてみた例も含めておきました。結果だけ記すと、0.522 ≤ ρ ≤ 0.644となり、正の相関があるといってよさそうです。

コラム　フィッシャー変換と逆変換を可視化する

　以下に再掲した図1のグラフを描くためのコードに加え、シミュレーションの結果も併せて表示するPythonプログラムを掲載しておきます。

図1（再掲）　母相関係数を区間推定するための考え方と手順

　ここでは、詳細までは解説しませんが、コード中のコメントなどを参考に、やっていることの流れは理解できると思います。参考程度にご覧ください（リスト1）。サンプルプログラムはこちらから参照できます。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます（Googleアカウントでのログインが必要です）。最初のコードセルをクリックし、［Shift］+［Enter］キーを押してコードを実行してみてください。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, pearsonr

rho = 0.58  # 母相関係数
n = 10  # サンプル数

### 理論値の作成 ###

# フィッシャー変換
z_mean = np.arctanh(rho)  # 平均
z_std = 1 / np.sqrt(n - 3)  # 標準偏差

# zの値を生成。ここでは、範囲を-1.2〜2.4とする
z_vals = np.linspace(-1.2, 2.4, 100)
pdf_z = norm.pdf(z_vals, loc=z_mean, scale=z_std)

# フィッシャー変換の逆変換
r_vals = np.tanh(z_vals)
pdf_r = pdf_z / (1 - r_vals**2)  # ヤコビアン補正

### サンプリングした値の作成 ###

count = 10000 # 繰返し回数

# サンプリングした相関係数を記録するための変数
r_samples = np.empty(count)

# 共分散行列
cov = [[1.0, rho], [rho, 1.0]]

# 2変量正規分布からサンプルを生成
for i in range(count):
    samples = np.random.multivariate_normal(mean=[0, 0], cov=cov, size=n)
    r_samples[i], _ = pearsonr(samples[:, 0], samples[:, 1])

# フィッシャー変換
z_samples = np.arctanh(r_samples)

# 理論値のグラフ
plt.figure(figsize=(10, 6))
plt.plot(r_vals, pdf_r, linewidth=2)
plt.plot(z_vals, pdf_z, linewidth=2)

# サンプルのヒストグラム
plt.hist(r_samples, bins=100, density=True, alpha=0.5)
plt.hist(z_samples, bins=100, density=True, alpha=0.5)

# 描画
plt.ylim(0.0,2.0)
plt.xlim(-1.2, 2.4)
plt.ylabel("Density")
plt.show()

リスト1　フィッシャー変換と逆変換を可視化した例
「理論値の作成」の部分では、まず、母相関係数rho=0.58とサンプルサイズn=10を基に、フィッシャー変換を行って平均と標準偏差を求め、正規分布の確率密度関数の値pdr_zを作成する。それを基にフィッシャー変換の逆変換を行って相関係数の確率密度関数の値pdf_rを作成している。ヤコビアン補正とは、変換前と変換後の（微小な）区間の面積を等しくするための補正のこと（用語の詳細は連載範囲を超えるので割愛するが、ここでpdf_zに掛けている1 / (1 - r_vals**2)は、空間の伸び縮み具合を示す係数で、「確率密度が正しく変換されるように調整するためのもの」と考えればOK）。
「サンプリングした値の作成」の部分では、母相関係数がrho=0.58となるような2つの正規分布からランダムにn=10個のサンプルを取り出し、相関係数を求めてr_samplesに10,000回記録する。さらに、それらをフィッシャー変換して正規分布で近似した値z_samplesを作成する。後は理論値のグラフ（折れ線グラフ）とサンプルのヒストグラムを描くだけ。

　NumPyやSciPyにはフィッシャー変換や逆変換を行う関数はありませんが、フィッシャー変換はarctanh（逆双曲線正接）関数で求められ、フィッシャー変換の逆変換はtanh（双曲線正接）関数で求められるので、numpyモジュールで利用できるそれらの関数を使っています。実行結果は以下のようになります（図5）。

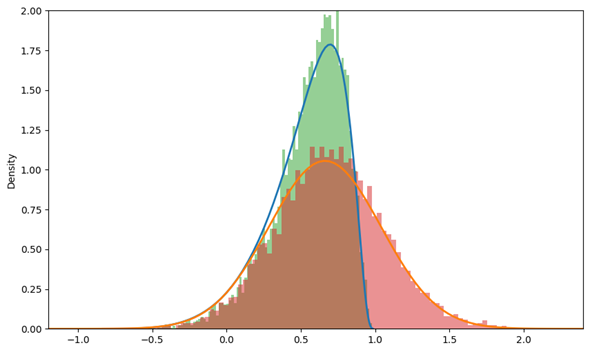図5　フィッシャー変換と逆変換を可視化した結果
オレンジの曲線（山の低い曲線）がフィッシャー変換によって求められた平均と標準偏差を基に描画した正規分布。ブルーの曲線（山の高い曲線）がフィッシャー変換の逆変換により描画した相関係数の理論的な分布。緑のヒストグラム（山の高いヒストグラム）は母相関係数0.58の2つの正規分布からランダムに10個のサンプルを取り出し、相関係数を10,000個求めたものをヒストグラムにしたもの。それをフィッシャー変換したものが、ピンクのヒストグラム（山の低いヒストグラム）。

　今回は、母集団が正規分布すると考えられる2つの群について、母相関係数を区間推定する方法を見ました。相関係数の分布には偏りがあるので、まず、フィッシャー変換を行って正規分布で近似し、信頼区間を求めました。その結果を基にフィッシャー変換の逆変換を行えば、相関係数の信頼区間が求められるというわけです。Excelにはフィッシャー変換のための関数が用意されているので、操作についてはそれほど難しくはなかったと思います。

　次回は区間推定の最終回としてサンプルサイズの決め方を見ることにします。次回もお楽しみに！

この記事で取り上げた関数の形式

　関数の利用例については、この記事の中で紹介している通りです。ここでは、連載で初出となる関数の基本的な機能と引数の指定方法だけを示しておきます。

信頼区間を求めるために使った関数

「やさしい推測統計（区間推定編）」