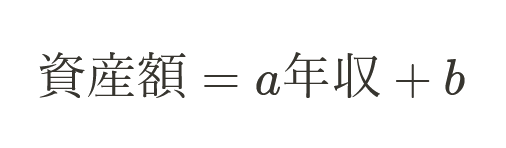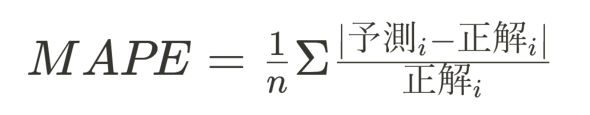”美しい仮定”は精度を向上させる――「回帰分析」には対数(log)変換が有用な理由:「AI」エンジニアになるための「基礎数学」再入門(16)
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。今回は「回帰分析」には対数変換を用いるとよい理由について解説します。
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す本連載『「AI」エンジニアになるための「基礎数学」再入門』。前回は最小二乗法および回帰分析について解説しました。
今回のテーマは、有用なケースが多いのでぜひ覚えてほしいテクニック「対数変換」です。前回の回帰分析に使えるものですが、「なぜ有用なのか?」についても解説します。
回帰分析の復習
前回学んだ単回帰分析について簡単に復習します。単回帰分析は、「y = ax + b」という数式である値を予測するものでした。例として、以下のような課題を与えられたとします。
- 課題:年収からその人の資産額を推測せよ
- 目的変数yが資産額
- 説明変数xが年収
| Name | y:資産額(万円) | x:年収(万円) |
|---|---|---|
| A | 300 | 1000 |
| B | 240 | 800 |
| …… | …… | …… |
単回帰分析なら次のような数式を仮定します。
この仮定の下で、データからa,bを求めることで数式を完成させるのが単回帰分析でした。この仮定をもう少し深く考察します。
単回帰分析の深掘り
数式(1)の両辺を“年収”で微分してみます。
数式(2)から何を読み取れるかというと、aは固定値なので「変化量の比は一定」ということです。すなわち、本仮定は次のようなことを言っているも同然だということになります(aを適当に0.3として、低所得/高所得者で考えてみましょう)。
- 年収100万円の人の年収が10万円上がれば資産額は3万円増える
- 年収100万円の人の年収が1000万円上がれば資産額は300万円増える
- 年収1000万円の人の年収が10万円上がれば資産額は3万円増える
- 年収1000万円の人の年収が1000万円上がれば資産額は300万円増える
つまり「ベースとなる年収に限らず、同じだけ年収が上がれば、同じだけ資産額は増える」という仮定です。この仮定は本当に正しいのでしょうか。これには少し違和感があります。一方、例えば次のような仮定の方が美しい、つまりシンプルかつ正しそうではないでしょうか。
- 年収が10%上がれば、資産額は10%上がる
- 年収が20%上がれば、資産額は20%上がる
このような仮定の方が現実世界に当てはまることが多いのです。しかし、この仮定を置くにはどうしたらよいでしょうか?
答えは連載第5回で学んだ「対数変換」です。対数を用いて次のような数式を考えます。
こうするだけで前述の“美しい仮定”が出来上がります。理由は後述するので、まずは「本当に精度が上がるのか?」を確認します。
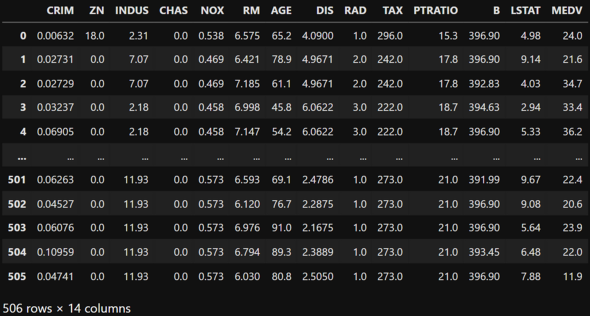
使用データ(ボストンの住宅価格データ)の説明
ボストンの住宅価格データは統計学や機械学習の初学者用チュートリアルによく使用されるオープンデータです。
配布元はカーネギーメロン大学で、ライセンス指定はありません。
【基本情報】
- 作成者:Harrison, D. and Rubinfeld, D.L. 'Hedonic prices and the demand for clean air', J. Environ. Economics & Management, vol.5, 81-102, 1978.
- タイトル:Boston Housing Data
- 公開日:July 7, 1993
- URL:http://lib.stat.cmu.edu/datasets/boston.txt
- CRIM:町別の「犯罪率」
- ZN:広い家(2万5000平方フィート以上)の割合
- INDUS:町別の「非小売業の割合」
- CHAS:チャールズ川に隣接しているかどうか(区画が川に接している:1、そうでない:0)
- NOX:「NOx濃度(0.1ppm単位)」=一酸化窒素濃度(parts per 10 million単位)
- RM:1戸当たりの「平均部屋数」
- AGE:古い家(1940年より前に建てられた)の割合
- DIS:5つあるボストン雇用センターまでの加重距離
- RAD:主要高速道路へのアクセス性指数
- TAX:1万ドル当たりの「固定資産税率」
- PTRATIO:町別の「生徒と先生の比率」
- B:「1000(Bk - 0.63)」の二乗値。Bk=「町ごとの黒人の割合」を指す(※人種差別の問題を含んでいる可能性があることに留意)
- LSTAT:低所得者人口の割合
- MEDV:「住宅価格」(1000ドル単位)の中央値
今回はDISを使ってMEDVを予測する単回帰分析をします。準備として以下のようにデータを読み込んでおきましょう(※機械学習用ライブラリ「sklearn」にはボストン住宅価格を簡単に読み込めるメソッドが用意されています)。
import pandas as pd from sklearn.datasets import load_boston boston = load_boston() df = pd.DataFrame(boston.data, columns=boston.feature_names) df["MEDV"] = boston.target
単回帰分析とその精度
単回帰分析を始める前に、DISとMEDVの相関を確認します。
とても1本の直線を引いたところでうまく予測できそうにありません。特にグラフ右上の方に点在するデータにいえることです。ひとまず、単回帰分析をしてみましょう。
通常の単回帰分析
Pythonにおける単回帰分析は、次のように簡単です。
from sklearn.linear_model import LinearRegression # 線形回帰(単回帰/重回帰)用クラス
X = df[["DIS"]]
y = df["MEDV"]
model = LinearRegression()
model.fit(X, y) # 学習
print("MODEL: MEDV = {0:.1f} DIS {1:+.1f}".format(model.coef_[0], model.intercept_))
# MODEL: MEDV = 1.1 DIS +18.4
ここで出来上がったモデル(数式)の精度を確認します。精度には、現場でよく使われる指標「MAPE」(Mean Absolute Percentage Error:平均絶対パーセント誤差)を使用してみます。
MAPEは端的にいうと、「1予測当たり平均で何%の誤差(正解の大きさ基準)があるか」が読み取れるものです。計算します。
# modelは学習済みの状態で実行
pred = model.predict(X) # 予測
# MAPEの計算
pe = (pred - y)/y
mape = abs(pe).mean()
print("MAPE = %.3f" % mape)
# 0.333
どうやら通常の単回帰分析では、1予測当たり平均で33.3%の誤差が発生しているようです。
対数変換を用いた単回帰分析
対数変換を用いた単回帰分析を確認します。
X = df[["DIS"]]
X_log = np.log(X + 1) # log(0)は計算できないので+1をしている
y = df["MEDV"]
y_log = np.log(y + 1)
model = LinearRegression()
model.fit(X_log, y_log)
model_desc = "MODEL: log(MEDV+1) = {0:.1f} log(DIS+1) {1:+.1f}".format(model.coef_[0], model.intercept_)
print(model_desc)
# MODEL: log(MEDV+1) = 0.4 log(DIS+1) +2.5
「精度を確認します」といきたいところですが、現状では対数変換されているので計算されたMAPEは単純比較できません。そこでlogを外します。
「log(y+1)=y'」のとき、「y+1=ey'」となるので、Pythonで次のように記述するとlogを外すことができます。
y = df["MEDV"] # 元のy y_log = np.log(y + 1) # 対数変換後のy np.exp(y_log) - 1 # y_logを元のyに戻す処理
対数の外し方が分かったところで、MAPEを確認してみましょう。
pred_log = model.predict(X_log)
pred = np.exp(pred_log)-1
pe = (pred - y)/y
mape = abs(pe).mean()
print("MAPE = %.3f" % mape)
# MAPE = 0.286
なんとMAPEが33.3%から28.6%まで下がりました。この現象の要因について考察します。
対数変換すると、なぜ精度が向上するのか?
「単回帰分析の深掘り」の部分と同様に対数変換版の単回帰分析の数式を確認していきます。数式(3)は次のようなものでした。
両辺を“年収”で微分してみましょう。
このままではよく分からないので、ひとまず今度は両辺を“資産額”で微分してみます。
数式(5''')から読み取れるのは、仮定「変化割合の比が一定」が置かれているということです。
つまり前述の、下記のように美しい仮定が対数変換をするだけで設定できていることが分かります。
- 年収が10%上がれば、資産額は10%上がる
- 年収が20%上がれば、資産額は20%上がる
今回はボストンの住宅価格データを例に対数変換版の単回帰分析を試しました。
これ以外にも対数変換が適しているデータは世の中にたくさんあります。むしろ「通常の単回帰分析が当てはまることの方が少ない」ということは大切なのでぜひ覚えておいてください。
対数変換が適しているケース
最後におまけで対数変換が適しているケースを1つ紹介します。

横軸:ワインの生産年、縦軸:log(ボルドーワインの価格)(Ashenfelter,Orley,David Ashmore, and Robert Lalonde.1995.“Bordeaux Wine Vintage Quality and Weather***.”http://www.liquidasset.com/orley.htm)
ちまたで有名な「アッシェンフェルターのワイン方程式」の原論文からの引用です。生産年とlog(価格)は比例関係があるように見えます。言い換えれば、「年数が深まるごとにボルドーワインの価格は“指数的”に上昇する」ことになります。
これを「ヴィンテージワインはコスパが悪いな」と思うか、「ヴィンテージワインの価値は指数的に高まるのか! あらためて素晴らしい!」と思うかは皆さんにお任せします。
まとめ
- 通常の回帰分析は「変化量の比が一定」という仮定を置いている
→しかし、この仮定が当てはまるケースは現実世界では少ない - 対数変換を施した回帰分析は「変化割合の比が一定」という仮定を置いている
→現実世界でよく当てはまる
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
![[AI・機械学習の数学]微分法を応用して、回帰分析の基本を理解する](https://image.itmedia.co.jp/ait/articles/2006/04/news013.jpg) [AI・機械学習の数学]微分法を応用して、回帰分析の基本を理解する
[AI・機械学習の数学]微分法を応用して、回帰分析の基本を理解する
微分の考え方と計算方法を理解したら、次は微分の公式を押さえて活用してみよう。幾つかの公式を紹介し、応用例として回帰分析を行うための最小二乗法について基本的な考え方を見ていく。![[AI・機械学習の数学]偏微分の基本(意味と計算方法)を理解する](https://image.itmedia.co.jp/ait/articles/2007/14/news021.jpg) [AI・機械学習の数学]偏微分の基本(意味と計算方法)を理解する
[AI・機械学習の数学]偏微分の基本(意味と計算方法)を理解する
「偏微分」って何? いかにも難しそうな名前だが、微分を理解していれば意外に簡単。前回までの知識を踏まえて、今回は偏微分の意味と計算方法を理解しよう。![[AI・機械学習の数学]偏微分を応用して、重回帰分析の基本を理解する](https://image.itmedia.co.jp/ait/articles/2007/28/news014.jpg) [AI・機械学習の数学]偏微分を応用して、重回帰分析の基本を理解する
[AI・機械学習の数学]偏微分を応用して、重回帰分析の基本を理解する
これまでに見てきた、説明変数が1つだけの回帰分析と偏微分の基本知識を踏まえて、複数の説明変数がある重回帰分析を行うための基本的な方法を理解しよう。