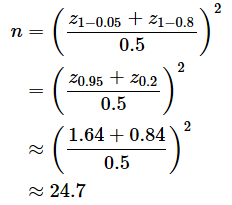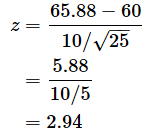試験の平均が60点より大きいか調べたい 〜 Z検定（母平均の検定）：やさしい推測統計（仮説検定編）

平均値の検定についての基本的な考え方

　最初に「母平均がある値と異なっているかどうかを知りたい」ということが、どのような場面での関心事であるかを確認しておきましょう。タイトルに「試験の平均が60点より大きいか調べたい」（＝検定する）と書きましたが、その、「60点」「より大きい」というのはどのような根拠で現れたものか、ということです。

　ある学校で毎年行われる試験では、これまでの経験から平均点が60点であったことが分かっているものとします。60点という値を恣意（しい）的に決めたわけではない、ということですね。「より大きい」と考えたのも、なんとなくではなく、例えば、授業の進め方を改善したので、同様の試験であれば、それまでよりもいい成績が取れるはずだ、その効果を確かめたい、と考えたからです（図1）。

図1　授業の改善により、平均点が上がったかを調べたい
授業を改善した結果、平均点（母平均）が60点よりも上がったことを確かめたい。ただし、過去のデータや経験などから平均点は60点であることが分かっており、生徒の能力と試験の難易度はこれまでと変わらないものとする。

　授業の改善と試験の例はいささか作為的ですが、このような例は、さまざまな領域で見られます。製品の耐久性が改善されたか、というのもその一例です。例えば、PCの記憶装置として一般的に使われているSSD（Solid State Drive）の寿命はTBW（Total Bytes Written）という指標で表されます。これまでの製品では、600TBW（600テラバイトまでの書き込みが可能）だと経験的に分かっているものとして、データを書き込むためのプログラムを改善したため、TBWが改善されたと考えられる場合などです。

　次に、前提についても確認しておきましょう。まず、生徒の基本的な能力や試験の難易度は毎年変わらず、成績は正規分布するというのが大前提です。ただし、サンプルサイズがある程度大きければ（一般に30以上と言われます）、母集団が正規分布していなくても、平均値の検定ができます。これは、中心極限定理を根拠としています。

　このように、母平均がある値と異なっているか（より大きいか／より小さいか）を吟味するための検定を平均値の検定と呼びます。平均値の検定は、母集団の分散が既知である場合と、未知である場合で方法が異なります。

　後でこれらの違いを見ていきますが、まずは仮説検定の手順に沿って帰無仮説を立てるところから始めましょう。図1のような試験の例で考えてみます。

平均値の検定での帰無仮説と対立仮説

　試験の例では、帰無仮説と対立仮説は以下の通りです。既に分かっているこれまでの平均点をμ₀＝60とし、改善された授業を受けた場合の母平均をμ₁とします。

　授業の進め方を改善したことにより、平均点が上がるものと想定されますが、まず、帰無仮説として母平均は60点であるという仮説を立てます。前回もお話ししたように、帰無仮説は「無に帰したい」仮説、つまり、棄却したい仮説ですね。帰無仮説が棄却できれば、「母平均は60点より大きい」という対立仮説を採用できるというわけです。ここでは、「異なる」ということではなく「より大きい」ということを言いたいので、片側検定を行うことになります。

　調査に先立って、サンプルサイズを見積もっておく必要があるので、次に整理しておきます。重要なことですが、やや煩雑になるので、平均値の検定の計算方法を先に知りたい方は取りあえず読み飛ばして、平均値の検定 〜 母分散が既知の場合に進んでいただいても構いません（でも、後でちゃんと戻ってきてください）。

平均値の検定での効果量とサンプルサイズ

　効果量とサンプルサイズの見積もりについて整理しておきます。まず、Cohen's dと呼ばれる指標を以下の式で求めます。

　μ₁は想定される母平均の値、σは既知の母標準偏差です。このことから、Cohen's dは「標準偏差と比べて差がどの程度なのか」を表すことが分かります。標準偏差で割っているということは、標準化を行い、集団や値の単位が異なっても比較できるようにしているということですね。

　例えば、教員のこれまでの経験から、平均点が5点程度上がるものと思われたとします。つまりμ₁＝65と考えられる場合ですね。σ＝10であるものとすると、

となります。サンプルサイズは以下の式で求めます。

　有意水準をα＝0.05、検出力を1−β＝0.8とすれば、

という結果が得られます。z_0.95≈1.64とz_0.2≈ 0.84という値は、ExcelのNORM.S.INV関数に0.95や0.2という値を指定するだけで求められます。結果はn＝24.7ですが、小数点以下を切り上げてn＝25としましょう。

　ここまでの計算については、サンプルファイルにまとめてあるので、こちらからダウンロードしたファイルを利用し、［サンプルサイズの計算］ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。操作方法は図2の中に記してあります。

図2　平均値の検定での必要なサンプルサイズを求める
（1）式で求めたCohen's dの値を基に、（2）式で必要なサンプルサイズを求める。結果は25となった。

　なお、両側検定の場合は、z_1−αの代わりに、z_1−α/2の値を使います。ちなみに、α＝0.05の場合、z_1−α/2＝1.96となり、n＝32という結果が得られます。

　母分散が未知の場合は、過去に得られた標準偏差や予備調査で得られた標準偏差を（1）式のσの代わりに使います。正確には、非心t分布と呼ばれる分布（中心が0ではないt分布）を使って計算するのですが、（1）式で近似できます。ただし、サンプルサイズが小さい場合（おおむね30未満の場合）は、＋2程度しておくといいでしょう。また、母分散に関して過去の知見などがなく、標準偏差が仮定できない場合は、効果量をやや小さめに見積もって、サンプルサイズを多めに取るのが安全です。

　なお、Excelには非心t分布の確率密度関数や累積分布関数の値を求める関数がないので、Excelを使って正確にサンプルサイズを計算するのはかなり面倒です。そこで、Pythonを使ってサンプルサイズを求める例をこちら（サンプルファイル）に置いておきます。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます（Googleアカウントでのログインが必要です）。最初のコードセルをクリックし、［Shift］+［Enter］キーを押してコードを実行してみてください。片側検定の場合n＝27という結果が表示されます（(1)式で近似した値＋2となっています）。なお、ここでは詳細な説明はしませんが、サンプル中に簡単な解説と、検出力を可視化した例を含めてあります。興味のある方はご参照ください。

平均値の検定をやってみよう（母分散が既知の場合）

　それでは、平均値の検定に取り組みましょう。これまでの経験から平均μ₀が60点、標準偏差σが10点と分かっている試験があるとき、改善された授業を受けた生徒が、同様の試験で以下のような点数を取ったものとします（架空のデータです）。

　これらのサンプルの平均

は65.88です。

　帰無仮説と対立仮説を再掲します。改善された授業を受けた場合の母平均をμ₁とすると、

　検定の計算では、検定統計量を求める→P値を求める、という計算を行うのですが、その方法については後で解説することにします。実は、Excelでは、そういった計算を一切行わなくても、Z.TEST関数を使うだけで平均値の検定ができてしまう（P値が求められる）からです。というわけで、結果を先に見ておきましょう。サンプルファイルの［平均値の検定 (母分散が既知)］ワークシートを表示し、図3のように、セルD4に「=Z.TEST(B4:B28, 60, 10)」と入力するだけです。

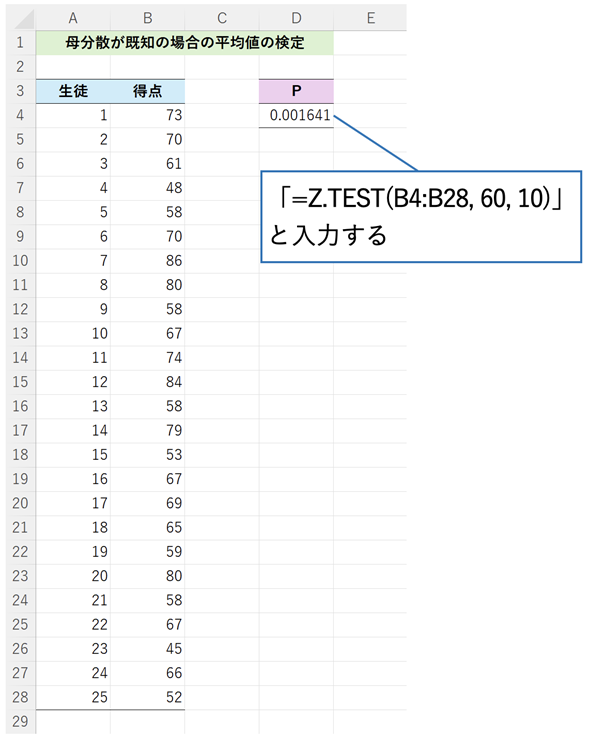
図3　母分散が既知の場合の平均値の検定（Z検定）を行う
Z.TEST関数には、データの範囲（ここではB4:B28）と、帰無仮説で想定した母平均（60）、母標準偏差（10）を指定する。計算の結果、P値が返される。

　図3の結果を見ると、P＝0.001641 ≤ 0.01なので、1％有意となり、帰無仮説が棄却されます。サンプルファイルの［平均値の検定 (母分散が既知・作成例)］ワークシートには、信頼区間と事後の効果量の計算も含めてあるので、気になる方は参照してみてください。

　信頼区間の求め方はこちらをご参照ください。ちなみに、μ₁の信頼区間は、61.96 ≥ μ ≥ 69.80で、事後の効果量（Cohen's d）は0.535（サンプルの不偏標準偏差を使って計算）となっています。ただ、今回の例は架空の事例なので、これ以上のことは言えませんが、実際には、同様の調査や研究と比較して、信頼区間が狭く、効果量が大きければ対立仮説が強く支持できると考えられます。

　なお、対立仮説がμ₁ < μ₀の場合（例えば、母平均は60点より小さい、などの場合）、左側確率を求める必要があるので「=1-Z.TEST(B4:B28, 60, 10)」のように、1から引いておきます。また、両側検定を行う場合は、いずれかの値の小さい方を2倍すればよいでしょう。つまり「=2*MIN(Z.TEST(B4:B28, 60, 10), 1-Z.TEST(B4:B28, 60, 10))」となります。

平均値の検定（母分散が既知の場合）の計算方法

　では、Z.TEST関数でどのような計算が行われているのかを確認しておきます。数式が苦手な方はあまり気にせず、読み飛ばしてもらっても構いません。母分散が既知の場合、まず、以下の統計量zを求めます。

　σ/√nで割っているのは、平均が0、分散が1になるように（標準正規分布になるように）調整するためです。この計算は母平均の信頼区間を導き出すときにもやった計算です。（3）式に

を当てはめてみます。

　標準正規分布のz＝2.94に対する右側確率を求めます。1から、以下の式で表される左側確率（累積分布関数の値）を引けば求められます（確率分布編で学んだこちらの式でμ＝0, σ＝1として、xを上のzと読み替えたもの）。

　erfは誤差関数と呼ばれる関数ですが、（4）式の値を四則演算だけで求めるのは難しいので、ExcelのNORM.S.DIST関数を使って求めましょう。どのセルでもいいので「=1-NORM.S.DIST(2.94, TRUE)」と入力してみると、0.001641という答えが得られます（Google スプレッドシートでは、「=1-NORM.S.DIST(2.94)」と指定します）。Z.TEST関数の結果と一致していますね。

　これまでの計算を可視化しておきます（図5）。グラフはPythonで作成してあります（前述のサンプルファイルに含めてありますが、可視化が目的なので、コードの詳細についての説明は割愛します）。

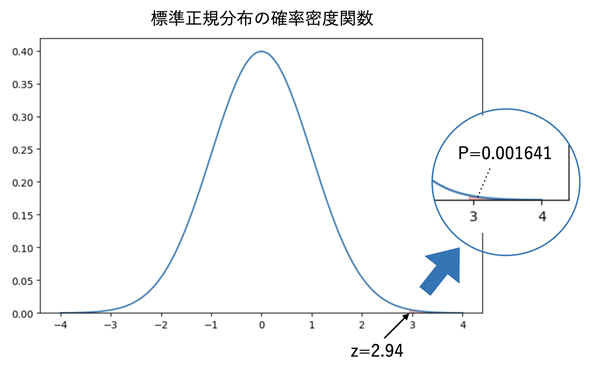
図4　平均値の検定を可視化する
標準正規分布の確率密度関数で、z＝2.94点よりも右側（上側）の累積確率（オレンジ色の部分の面積）はP＝0.001641となる。かなり小さいので右側にも拡大した図を示してある。帰無仮説が正しいとすれば、かなり珍しいことが起こった、ということが分かる。

平均値の検定をやってみよう（母分散が未知の場合）

　実際には、母分散が既に分かっているという場合はあまりないかと思われます。そのような場合（母分散が未知の場合）には、サンプルの不偏分散を指定し、t分布を利用して検定を行います。こちらの方がよくある事例ですね。ただ、残念ながらExcelには、このような場合に対応する検定のための関数がないので、以下の手順に従って計算する必要があります。

　sはサンプルから求めた不偏分散です。これはSTDEV.S関数で求められます。

　では、Excelで計算してみましょう。データは母分散が既知の場合の例と同じものを使うことにします。サンプルファイルの［平均値の検定 (母分散が未知)］ワークシートを表示し、図5に示した式を入力しましょう。

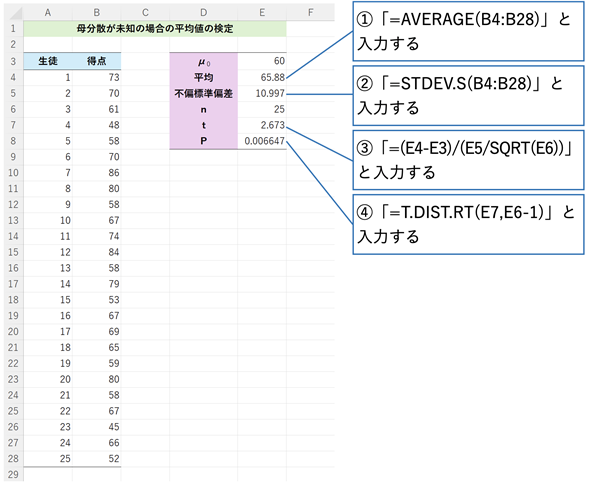
図5　母分散が未知の場合の平均値の検定を行う
セルE4にAVERAGE関数で平均を、セルE5にSTDEV.S関数で不偏標準偏差を求める。（5）式で検定統計量tを求めるのがセルE7に入力した「=(E4-E3)/(E5/SQRT(E6))」。セルE8に入力したT.DIST.RT関数でtの値に対する右側確率を求める。

　結果はP＝0.006647 ≤ 0.01なので、1％有意となり、帰無仮説が棄却されます。なお、信頼区間は、61.34 ≥ μ≥ 70.42です（サンプルファイルの［平均値の検定 (母分散が未知・作成例)］ワークシートに含めてあるのでぜひ参照してみてください）。

　対立仮説がμ₁ < μ₀の場合（例えば、母平均は60点より小さい、などの場合）にも1つの式で計算できる表にするには、t値（セルE7）の絶対値を使い、セルE8の式を「=T.DIST.RT(ABS(E7), E6-1)」とするのが簡単です（t分布は左右対称な分布なので）。両側検定を行う場合は、T.DIST.2T関数が使えるので、セルE8の式は「=T.DIST.2T(E7,E6-1)」となります。

　今回は、母分散が既知の場合と未知の場合に分けて、平均値の検定方法を解説しました。

　ところで、今回の事例を見て、もっと違った方法があるのでは、と思った方もおられるかもしれません。例えば、これまでの方法で授業を受けた生徒と新しい方法で授業を受けた生徒の2つの群を作って、それぞれの試験の平均値の差を検定する、という方法があります。同じ試験問題で差が比較できるので、その方が条件をよりよく統制できます。というわけで、次回は、そのような場合に使われる検定（母平均の差の検定）に取り組みます。どうぞお楽しみに！

この記事で取り上げた関数の形式

　関数の利用例については、この記事の中で紹介している通りです。ここでは、連載で初出となる関数の基本的な機能と引数の指定方法だけを示しておきます。

平均値の検定（Z検定）を行うために使った関数

「やさしい推測統計（仮説検定編）」