Excelで学ぶ、やさしいデータ分析【仮説検定編】 〜 考え方とP値の基礎:やさしい推測統計(仮説検定編)
初歩から応用までステップアップしながら学んでいく『やさしいデータ分析』シリーズ第4弾がスタート。第1回は仮説検定の考え方や知っておくべきキーワード、今後の連載予定を紹介します。データ分析を実践的に役立てるための基礎をしっかり学んでみませんか?
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載『社会人1年生から学ぶ、やさしいデータ分析』のシリーズとして、「記述統計と回帰分析編」「確率分布編」「推測統計(区間推定編)」に続いて、今回から「推測統計(仮説検定編)」を開始します。2023年から始まった連載もおかげさまでいよいよ第4シーズンに突入です。
これからのお話は、仮説検定と呼ばれる分野に関するものとなります。そこで、仮説検定の考え方や留意点を簡単にお話ししておきましょう。仮説検定については、P値の取り扱いについて、さまざまな問題が指摘されており、誤解したまま使っていると結果の信ぴょう性が損なわれるので、最初に考え方と知っておくべきキーワードを解説します。
今回は初回ということもあり、新しい用語や考え方が幾つも出てきます。ところどころで戸惑うかもしれませんが、全てを一度で理解できなくても大丈夫です。これらは連載の中で何度も取り上げ、特に最初のうちは丁寧に分かりやすく説明します。今回は「そういうものがあるんだな」という気持ちで、まずは最後まで読んでみてください。
連載:
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」「推測統計(区間推定編)」に続く「推測統計(仮説検定編)」です。
この連載では、観測されたデータを基に、平均に差があるかどうか、分散に差があるかどうかなどを吟味するために、仮説検定を行う方法や適用時の留意点などを説明します。身近に使える表計算ソフト(Microsoft ExcelやGoogleスプレッドシート)を使いながら具体的に事例を見ていきます。
必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。
筆者紹介: IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。
仮説検定とは 〜 区間推定と仮説検定の概要
仮説検定編の連載に当たって、最初に、仮説検定の位置付けを確認しておきましょう。これまでの連載で学んだ内容と併せて、チャートにまとめておきます(図1)。
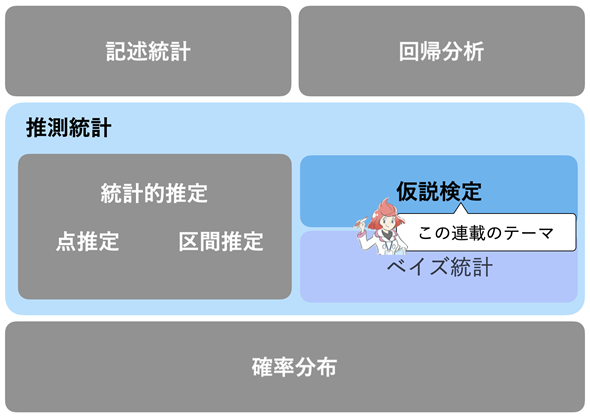
図1 この連載では仮説検定を取り扱う
白い字で書かれたものがこれまでの連載で学んできたもの。中でも確率分布は推測統計の基礎となり、区間推定の考え方は仮説検定と密接に関連している。なお、この連載の続編として「ベイズ統計編」も予定している。
仮説検定とは、文字通り、ある「仮説」を「検定(何らかの基準により正しいかどうかを判定)」することです。手順としては、まず、帰無仮説と呼ばれる仮説を立て、確率分布などを基に、その仮説が棄却されるかどうかを判断します。例えば、コイン投げについて、そのコインがイカサマでない(オモテとウラが等確率で出る)という仮説を立て、それが棄却されるかどうかを判断します。
より正確に言うと、仮説検定では、帰無仮説が正しいと考えられる場合に、サンプルとして得られたデータ以上に極端なデータが現れる確率を求めるということです。詳細については具体的な例で見ていきます。
これまでに学んできたさまざまな手法では、「正しい」「正しくない」といった判断を下すことはありませんでした。仮説検定では、明確な判断を下すような表現が使われるので、分かりやすい結論が得られるように思われます。しかし、「白でなければ黒」といった二律背反的な解釈が行われたり、根拠が希薄であっても、結論が一人歩きしてしまったりする問題が指摘されています。そこで、仮説検定に取り組むに当たって、そのような仮説検定を行う際に陥りやすい問題点についても解説することにします。
ところで「仮説が棄却されるかどうか」というのはヘンな表現ですね。素直に「仮説が支持されるかどうか」と言えばいいのにと思われるかもしれません。その辺りの意味についてもこれから見ていきます。また、仮説検定にまつわる誤解などについても見ていきます。
仮説検定の「仮説」って何、「検定」ってどう計算するの?
前回の連載で見た区間推定は、母集団から取り出されたサンプル(標本)を基に、母平均や母分散などの母数を一定の幅を持たせて推定する、という手法でした。これから学ぶ仮説検定は、推測統計において、区間推定と表裏をなすような位置付けの手法です。まずは、仮説検定の基本的な考え方と手順から見ていきましょう。
帰無仮説 〜 「無に帰したい」仮説とは?
先ほどもお話ししたように、仮説検定では、まず帰無仮説と呼ばれる仮説を立てます。帰無仮説とは、「無に帰したい」仮説です。つまり、気持ちとしては否定したい仮説です。帰無仮説が棄却されれば、帰無仮説と対立する仮説、つまり対立仮説を採用する、というわけです。
仮説検定の基となる有意性検定の考え方を提唱したフィッシャーは、対立仮説を立てるという二律背反的な考え方を採っていませんでした。一方、ネイマンとピアソンは対立仮説を立て、帰無仮説が棄却されれば対立仮説を採用するという考え方(これが仮説検定)を採ります。
では、帰無仮説とはどのようなものでしょうか。具体例で見てみましょう。話を分かりやすくするため、コイン投げの単純な例で考えます。コイン投げでは、イカサマでない限り、オモテとウラが等確率(1/2ずつ)となるはずです(まれに立つこともあるかもしれませんが、それは考慮しないことにします)。しかし、あまりにもオモテが出すぎるような気がしたので「イカサマではないか」という疑いを持ったとします。
コインそのものがイカサマである、コイン投げの方法がイカサマである、といった可能性がありますが、ここではまとめて「コインがイカサマである」といった表現にします。
気持ちとしては、イカサマであるということを立証したいのですが、仮説検定では、逆に「このコインはイカサマではない」という帰無仮説を立てます。イカサマでなければ、コイン投げの結果は試行数がn、オモテの出る確率pが1/2の二項分布に従います。つまり、前提が具体的に決められるからです。一方の対立仮説は「このコインはイカサマである」ということになります。といっても、どの程度イカサマであるかは分かりません。対立仮説から出発しないのは、具体的な前提を決めづらいからです。
注意していただきたいのは、オモテが43回出たからイカサマだという帰無仮説を立てるわけではありません。それは本末転倒(後出しじゃんけんのようなもの)です。イカサマだという疑いが生じたので帰無仮説を立て、それを確かめるためにコインを投げて実験してみたところ、43回オモテが出た、ということです。
どの程度イカサマであるかを想定して、効果量(後述します)などを見積もることはありますが、仮説検定では、まず帰無仮説から出発します。なお、ベイズ統計では、イカサマである確率を事前確率として想定することができます。
帰無仮説はH0、対立仮説はH1で表されるので、以下のように箇条書きで表すことがよくあります。オモテが出る確率をpとして、確率を考慮した書き方にしてみます。HはHypothesis(仮説)の頭文字です。
- H0: このコインはオモテとウラが等確率で出る(p=1/2である)
- H1: このコインはオモテとウラが等確率では出ない(p=1/2でない)
H0とH1を見て、何か気付くことはないでしょうか。
- H2:このコインはオモテの出る確率が高い(p>1/2である)
という対立仮説も立てられることが分かりますね。どちらの仮説を対立仮説とするかは、実験や観察の目的によります。上の例では、オモテがよく出るような気がしているので、H2を対立仮説とした方が良さそうです。
なお、H1の場合は、オモテがよく出る場合とウラがよく出る場合を考える必要があるので、両側検定と呼ばれる方法を使います。一方のH2の場合は、オモテがよく出る場合だけを考えればいいので、片側検定と呼ばれる方法を使います(後述)。
帰無仮説を棄却するかどうかを決める方法は?
では、帰無仮説を棄却するか、棄却しないかをどのようにして決めるのでしょうか。サンプルとして得られた値が帰無仮説での分布から大きく外れていれば、帰無仮説が棄却できる=対立仮説を採用する、というのが仮説検定の論理です。前掲した図2の例で具体的に計算してみます。
オモテとウラが等確率(p=1/2)で出るコインをn=70回投げたときの確率分布は二項分布で表されます。その場合、オモテが43回以上出る確率Pは、ExcelのBINOM.DIST関数を使って求められます。
サンプルファイルをこちらからダウンロードし、[二項検定]ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。操作方法は図3に記す通りです。結果はP ≈ 0.0361となるはずです。Google スプレッドシートでも操作は同じです。
ここで、小文字のpは個々の試行の確率(つまり、1回の試行でオモテが出る確率)を表しますが、大文字のPは、二項分布の累積確率(つまり、オモテが43回以上出る確率)を表していることに注意してください。
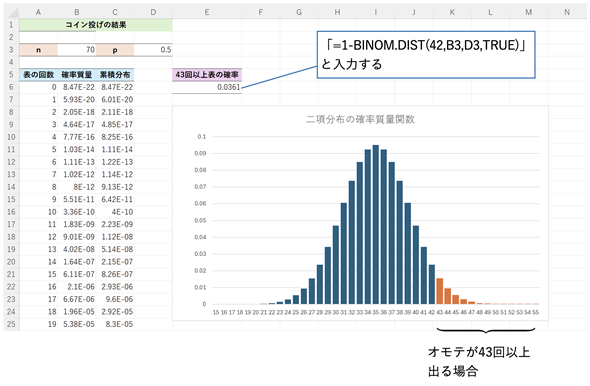
図3 オモテが43回以上出る累積確率と二項分布の確率密度関数のグラフ
オモテが43回以上出る確率は、1から、オモテが42回まで出る累積分布関数の値を引いたものとなる。セルE6に入力した「=1-BINOM.DIST(42,B3,D3,TRUE)」がその値を求めるための式。BINOM.DIST関数の引数には、成功数(42)、試行数(B3)、成功確率(D3)、累積分布関数の値を求めることを表すTRUEを指定する。
図には、Pの値(P値)を可視化するために、二項分布の累積分布関数のグラフも併せて示してあります(ただし、端の方は値が小さくなり見づらいので、オモテの回数が15回から55回までを表示してあります)。オモテが43回以上出る確率は右側のオレンジ色の部分の累積確率です。これは、1から、オモテが42回まで出る累積確率を引いても求められます。グラフの作成方法については、こちらを参考にしてください。
ここでは、片側検定を行うので右側確率だけを求めています。両側検定を行うのであれば、左側確率と右側確率の合計を求める必要があります。p=1/2ではないと言いたい場合は、p>0.5の場合とp<0.5の場合の両方を考える必要があるからです。
この例の場合は、43〜70の最も確率が高い値(図3では43の場合の確率)よりも小さな確率を全て合計するのが一般的な方法です。簡易的な方法として、右側確率と、43〜70に相当する左側の範囲(0〜27)の確率を合計することもあります。
さて、図3で求められた値はP ≈ 0.0361でした。コイン投げが二項分布に従うとすると、かなりまれなことが起こったということになります。ということは、p > 1/2である、と言えそうです。
一般に、P ≤ 0.05の場合「5%有意で帰無仮説を棄却する」と言い、対立仮説を採用します。この場合であれば「このコインはオモテの出る確率が高い」と結論付けるわけです(が、最初に少し触れたように、それには落とし穴もあります。後述します)。判断の基準とする値は有意水準と呼ばれ、αで表されます。一般にα=0.05またはα=0.01が使われます。
仮説検定に関する誤解と誤用
ここまで、二項分布を想定した仮説検定(二項検定)の手順を見ました。以下の通りです。
- 帰無仮説と対立仮説を立てる
- 帰無仮説が正しいと考えた場合の確率分布で、得られた事象以上に極端な事象の起こる累積確率(P値)を求める
- P ≤ 0.05あるいはP ≤ 0.01の場合は帰無仮説を棄却し、対立仮説を採用する
- P > 0.05であれば、帰無仮説が棄却できないので、対立仮説は採用できないとする
P値が0.0361だったので、5%有意で「オモテが出やすい」と判断することは、単純で分かりやすい半面、さまざまな落とし穴があります。それについて見ていきましょう。
帰無仮説が棄却される場合は?
P値が小さいということは「帰無仮説が正しいとすれば、めったに起こらないことが起こった」ということです。その場合、帰無仮説は支持しづらいので、帰無仮説を棄却します。
しかし、逆は必ずしも真ならず、です。めったに起こらないことが起こったからといって、(帰無仮説は棄却しますが)帰無仮説が間違っている、とも断言できません。また、対立仮説が正しいことが証明されたわけではありません。あくまでも、帰無仮説が間違っていて、対立仮説が正しいことの傍証の一つである、ということです。
現在では、P値だけを使って「有意なので差がある」と判断したり、対立仮説をそのまま採用したりすることを避けるのが一般的です。後述する効果量や検出力、信頼区間などを併せて示すのが望ましいとされています(統計的有意性とP値に関する米国統計学会の声明などを参照)。
帰無仮説が棄却できない場合は?
一方、P値が大きく帰無仮説が棄却できない場合でも、帰無仮説が採用できるというわけではありません。コイン投げの例で言うと、帰無仮説は「このコインはイカサマではない」でした。帰無仮説が棄却できないということは「このコインはイカサマではない」ことを否定できないということですが、かといって肯定されるわけでもありません。そのような場合には、「このコインはイカサマであるとは言えない」と表現します(イカサマでないとは言っていない)。
第一種の過誤と第二種の過誤について 〜 有意水準αと検出力1-β
仮説検定においては、第一種の過誤、第二種の過誤と呼ばれる、仮説に対する判断の誤りがあります。簡単に整理しておきましょう。日常的な火事と警報器の例と併せて示します(表1)。
| 帰無仮説を棄却 | 帰無仮説を棄却しない | |
|---|---|---|
| 帰無仮説が正しい | 第一種の過誤(α) | 正しい |
| 対立仮説が正しい | 正しい | 第二種の過誤(β) |
| 警報器が鳴る | 警報器が鳴らない | |
|---|---|---|
| 火事が起こっていない | 第一種の過誤(α) | 正しい |
| 火事が起こっている | 正しい | 第二種の過誤(β) |
第一種の過誤は間違って警報を出してしまうのと同じなので、FALSE ALARM(誤警報)と呼ばれることもある。また、ウイルスに感染していないのに検査で陽性になるのと同じなので、偽陽性と呼ばれることもある。無実の人を有罪にしてしまう冤罪も同じ誤り。逆に、第二種の過誤はウイルスに感染しているのに検査をすり抜けてしまうことや、真犯人を無罪にしてしまう誤りと同じ。
第一種の過誤とは、帰無仮説が正しいのに、帰無仮説を棄却してしまう誤りで、その確率を有意水準と呼びαと表します。αの値は、実験や調査の前に0.05ないし、0.01と決めておくのが本来の考え方です(結果を見てから、P ≈ 0.0361だったから、α=0.05にしよう、というのは本末転倒です)。また、P値は第一種の過誤を犯す確率ではありません。前にもお話ししたように、P値が小さいということは、あくまでも、帰無仮説が正しいとすれば、あまり現れないような(αで表されるような範囲に入る)珍しい結果が得られたということでしかありません。
一方の第二種の過誤とは、帰無仮説が誤っている(対立仮説が正しい)のに、帰無仮説を棄却しない誤りです。その確率はβで表します。つまり、差があるのに正しく検出できないという誤りと考えられます。従って、この確率を1から引いた1−βは、帰無仮説が誤っている(対立仮説が正しい)ときに、それを正しく検出できる確率ということになります。そのため、1−βを検出力と呼びます。
仮説検定においては、P値だけでなく、検出力も重要です。一般に、検出力は80%程度が推奨されますが、医学などで人命に関わる場合には90%などの値が使われることもよくあります。検出力は次にお話しする効果量とともに、適切なサンプルサイズを決めるのに使われます。
効果量とサンプルサイズについて
効果量とは、どの程度の差があると想定されるか、といった値です。効果量の目安としては、平均の差などではCohen's d、比率の差などではCohen's hといった値がよく使われます(表2)。
| Cohen's d, hの値 | 効果の大きさ |
|---|---|
| 0.2 | 小 |
| 0.5 | 中 |
| 0.8 | 大 |
効果量の目安としてよく使われるCohen's dの値とCohen's hの値。これらの値を基に適切なサンプルサイズの計算なども行われる。ちなみに、Cohen(コーエン)は数学者のポール・コーエンではなく、心理学者・統計学者のジェイコブ・コーエン。
効果量は、過去の経験などから適切な値を決める必要があります。また、表2はあくまでも目安なので、0.5だから効果は中程度としゃくし定規に決めるのは避けるべきです。その分野で蓄積された知見や同様の調査、実験と比較するなどして、解釈する必要があります(効果量を解釈する際に考慮すべきポイントなどを参照)。一般に、効果量が大きくなると、適切な結果を得るために必要なサンプルサイズが小さくなり、検出力も上がります。また、P値も小さくなります。
例えば、バスケットボールの選手と一般の人との身長差を調べる場合を想像してもらうといいでしょう。経験上、かなりの差があると思われるので、効果量を大きく見積もっておきます。そのような場合、数名ずつの小さなサンプルでも、P値が小さくなるものと考えられます。
一方、バスケットボールの選手とバレーボールの選手の身長差の場合は、一般人との場合に比べて、差が大きいとは考えにくいです。そのような場合には、効果量を小さく見積もって、ある程度サンプルサイズを大きくしないと適切な結果が得られません。
効果量を大きく見積もると、サンプルサイズもP値も小さくなるのであれば、大きく見積もっておいた方がいいんじゃないの、と思われるかもしれません。しかし、そのようにして見積もった小さなサンプルサイズで実験したときに、実際に得られた差が小さければP値は小さくなりません(有意にはなりません)。バスケットボールの選手とバレーボールの選手の身長差を大きく見積もって、小さなサンプルサイズで身長差を調べても差が出ないということです。
本来は、効果量と有意水準、検出力を基に適切なサンプルサイズをあらかじめ決めておきます。話が細かくなりますが、コイン投げの例で、以下のように想定した場合のサンプルサイズを求めてみましょう。
| 項目 | 値 | 備考 |
|---|---|---|
| p0 | 0.5 | 帰無仮説が正しい場合にオモテが出る確率 |
| p1 | 0.65 | 対立仮説が正しい場合にオモテが出る確率(見積もった値) |
| 効果量(Cohen's h) | 0.30 | p0とp1から計算される |
| 有意水準α | 0.05 | 帰無仮説を棄却するかどうかを判断するための基準となる確率 |
| 検出力1-β | 0.8 | 帰無仮説を正しく棄却できる確率 |
p0は帰無仮説が正しい場合にオモテが出る確率、p1は対立仮説が正しい場合にオモテが出る確率を見積もった値。ここでは、イカサマコインであって、オモテが0.65程度現れるのではないかと見積もっている。効果量はp0とp1を基に求められる(後述)。これらの値は、調査や実験を計画する段階で事前に決定しておくことが望ましい。
Cohen's hは、以下の式で求められます(この式は、pによる分散の歪《ゆが》みを軽減して効果量を求めるものですが、根拠についてはかなり難しいので、ここでは割愛します)。arcsinは正弦関数(sin)の逆関数で、ExcelではASIN関数で求められます。
二項検定で、適切なサンプルサイズを求めるための式は以下の通りです(正規近似による式)。
Z1−αやZ1−βは、標準正規分布の右側確率に対する確率変数の値です。これらは、NORM.S.INV関数で求められます。
では、Excelで計算してみましょう。サンプルサイズは大きめに見積もるべきなので、小数点以下は切り上げます。サンプルファイルの[サンプルサイズの計算]ワークシートを開き、図4に従って式を入力してみてください。
今回の事例で、コインを70回投げたのは、適切なサンプルサイズが67だったので、少し余裕を見てキリのいい数字にしたためです。
ちなみに、実験後に(1)式で効果量を求めると、当初の見積りよりもやや小さい0.231となります。観測された差は事前に想定していた差よりも小さかったということです。参考として、サンプルファイルの[サンプルサイズの計算(完成例)]のセルB13に実験後の効果量を求める式を入力してあります。
実際にオモテになったのが43回なので、p1=43/70=0.614です。この値は事前に想定したp1の確率(0.65)よりも小さいので、Cohen’s hを求めるまでもなく、実験後に求めた確率(効果量)がやや小さいことが分かります。が、Cohen's hは標準化された値なので、他の研究などと比較しやすくなります。
さまざまな仮説検定の方法 〜 この連載で取り扱う内容
今回は、新しい連載の概要と、仮説検定とはどのようなものであるかを紹介する回でしたが、効果量や検出力、適切なサンプルサイズなどについてかなり細かな話をしました。というのも、仮説検定では、P値だけで「差がある」または「差があるとは言えない」と単純に結論を出してしまう危険があるからです。上で触れた米国統計学会の声明でも、P値を禁止しているわけではありませんが、調査や実験の透明性を確保し、併せて、効果量や検出力、信頼区間などを示すことの必要性を述べています。
その上で、仮説検定の各種手法について、これから解説していきます。おおむね、表3のように進めていくつもりですが、話の流れによっては内容や事例などを変更することがあるかもしれません。
| 回 | テーマ | 主な内容 |
|---|---|---|
| 1(今回) | 推測統計(仮説検定編)の連載開始! | 仮説検定とは、仮説検定の進め方、仮説検定の落とし穴 |
| 2 | 母平均の検定 | 試験の平均がある値と等しいか |
| 3 | 母平均の差の検定 | 学校によって学力に差があるか |
| 4 | 母分散の検定 | 動画視聴時間のバラツキはある値と等しいか |
| 5 | 母分散の差の検定 | 新製品の品質は安定しているか |
| 6(番外編) | サンプルサイズや効果量を求めるための便利なツール | G*Power(検定力分析ソフトウェア)やPythonを使った事例の紹介 |
| 7 | 独立性の検定 | 出身地域と支持政党に関係はあるのか |
| 8 | 無相関の検定 | 排気量と中古車価格に関係はあるのか |
| 9 | 回帰式の検定 | 排気量と年式から中古車の価格は本当に決まるのか |
| 10 | 回帰式の係数の有効性を検定 | 中古車の価格に本当に影響しているのは何か |
| 11 | 中央値の差の検定 | 性別によってお小遣いの額は異なるのか |
| 12 | 分布の広がりの差の検定 | クセの強い先生と万人受けする先生の違いは? |
| 13 | 順位相関の検定 | 文系人間は本当に理系科目が苦手か |
| 14 | 分散分析超入門 | ヒントの与え方によって成績は変わるか |
内容や事例については、都合によって変更することがあるかもしれないが、取り上げる仮説検定の方法については、おおむね、この表の流れに沿って見ていくこととする。
今回は、仮説検定の流れに加え、しつこいぐらいに仮説検定の落とし穴についてお話ししてきました。今回の事例は仮説検定の流れを理解するために、比較的分かりやすい例を紹介しましたが、実際に調査や実験を行うと、さまざまな問題が起こることがあります。例えば、適切なサンプルサイズを計算して実験を行ったが、データの欠損などにより、そのサンプルサイズのデータが得られなかった場合などです。そういった場面も想定し、連載の中でも必要に応じて、仮説検定の落とし穴や、有意水準の設定、検出力、効果量、サンプルサイズの求め方などについてまた触れることとします。
次回からいよいよ本編。まずは、母平均の検定です。お楽しみに!
この記事で取り上げた関数の形式
関数の利用例については、この記事の中で紹介している通りです。ここでは、連載で初出となる関数の基本的な機能と引数の指定方法だけを示しておきます。
正弦関数の逆関数の値を求めるために使った関数
ASIN関数: 正弦関数の逆関数の値を求める
形式
ASIN(数値)
引数
- 数値: 正弦関数の値を−1〜1の範囲で指定する。
Copyright© Digital Advantage Corp. All Rights Reserved.

