「ずんだもん校正術」と「自分で実装する浮動小数点数値の加算」：Deep Insider's Eye　一色＆かわさきの編集後記

ずんだもん校正術（一色）

一色政彦（いっしきまさひこ）

一色政彦

　＠ITのDeep Insider編集部の編集長。1月の編集後記で書いた旅行計画の通り、春に新潟で日本酒を楽しんできました。新潟駅近くの今代司（いまよつかさ）酒造で酒蔵（さかぐら）見学に参加して甘口〜辛口の仕込み方の違いなど学んだ後、種類豊富な日本酒を試飲（テイスティング）でき、大満足でした。さらに、ぽんしゅ館 新潟駅店の「唎酒番所（ききざけばんしょ）」でも試飲。そこで「N-888」という白ワインのような日本酒に出会い、思わずネットで2本注文しちゃいました。まろやかな酸味と香りが印象的なので、機会があればぜひ試してみてください。夏休みには長崎・五島列島に行く予定なので、今度は魚をたっぷり堪能するぞぉ。

　いつもご愛読ありがとうございます。今や「AIで調べる」のが当たり前になり、Google検索の結果にも「AIによる要約（AI Overview）」が冒頭に表示されます。そんな時代にあっても、『AI・機械学習の用語辞典』『機械学習入門』『やさしいデータ分析（確率分布や区間推定など）』『Pythonクイズ』といった連載記事を読んでいただけていること、心から感謝しています。

　「記事なんて必要あるの？」という問いも出てきそうです。もちろん、AIには最速で答えが得られる便利さがありますが、基礎からしっかり学べる教科書や、人間が構成したチュートリアルには、理解を深めていく上での確かな価値があると思います。単発の質問と回答を繰り返すだけではなかなか身に付かない知識も、順を追って体系的に学ぶことで、しっかりと自分の中に積み上げていける――それが「記事」の強みだと考えています。

　例えば最近公開したPythonの「uv」入門記事は、初学者にとって必要なポイントを、筆者独自の視点から過不足なく整理した内容になっています。少し長めの記事ではありますが、多くの方に繰り返しご参照いただいており、大きな励みになっています。また、ロジスティック回帰の入門記事も、初学者でもつまずかずに理解できるよう、仕組みを筆者ならではの切り口で丁寧にかみ砕いて説明しました。この機械学習の入門連載も引き続き読んでいただけているようで、とてもうれしく感じています。

　さて、ここからが本題です。筆者は執筆中によく、「余計な文字を足す」「“て・に・を・は”などが抜ける」といった凡ミスをやらかします。そのため、1文字ずつ丁寧にチェックする必要があるのですが……正直、面倒です。もっと効率よくミスを見つけられないものでしょうか？　AIに頼る手もありますが、完璧とは言えませんよね。

　そこで、もう10年以上続けているのが「音声による校正」です。自分の声で読んでもよいのですが、それすら面倒なときもあります。

　そんな筆者が愛用しているのが、音声読み上げソフトウェア「詠太（えいた）」に付属するツール、「どこでも詠太」です。これは、クリップボードにコピーされたテキストを自動的に読み上げてくれるツールです。つまり、テキストエディタやWordなどで文章を選択し、［Ctrl］＋［C］キーを押してコピーするだけで、その内容をすぐに音声で再生してくれます。

「どこでも詠太」で［読み上げ設定］を開いた状態。閉じるとバーだけのコンパクト表示になり、邪魔になりません！

　ちなみに「詠太」はWindows専用です。今回ご紹介する内容も、Windows限定です。macOSやLinuxの方、ごめんなさい……。

　「便利に使っている」とはいえ、「もっと自然な声で読んでくれたらなぁ」と思っていたところで思い出したのが、ずんだもんです。無料のテキスト読み上げソフトウェア「VOICEVOX」で、キャラクター「ずんだもん」を使えば、自然な音声でテキストを読み上げてくれます。私の場合、このツールは既にインストール済みでした。

VOICEVOXで「ずんだもん（ノーマル）」を使っているところ

　あとは、テキストをコピーしたタイミングで、VOICEVOXが自動で読み上げてくれたら便利なのに……と思っていたところ、まさにそれを実現するツールが存在していました。

　上記のリンク先ページにある手順に従ってVoivoClipをインストールし、「VoivoClipNC.exe」を実行すれば、テキストをコピーするだけで、自動的に音声で読み上げてくれるようになります。「どこでも詠太」とほぼ同じ感覚で使えるのが魅力です。

VOICEVOXで「ずんだもん（ノーマル）」を使っているところ。シンプルなUIで［開始］／［停止］もワンクリック！

　ずんだもんに読んでもらえると、不思議と心が穏やかになります（笑）。とはいえ、細かな設定や使い勝手では、やはり「どこでも詠太」に軍配が上がります。そんなわけで、筆者は今のところ乗り換えてはいません。

　もし、「ずんだもん」ではなく「詠太」を使いたい場合は、日本語ワープロソフトウェア「一太郎」（プラチナ限定）の付属ツールとなるため、あらかじめ一太郎の「プラチナ版」を購入する必要があります。ただ、音声読み上げのためだけに“有償”ソフトウェアを買うのは、少しハードルが高いかもしれません。

　「“無料”で使いたい」「ずんだもんの声が好き！」という方には、今回紹介した「VOICEVOX＋VoivoClip」の組み合わせがお薦めです。

　最後に、少し補足します。今回は「音声による校正」にフォーカスしましたが、筆者自身は「読んで自然に聞こえるか、意味がスッと入ってくるか」という観点でも、原稿を最初から音読させることがあります。文章を“耳で聴く”ことで、論理の飛びや言葉の引っかかりに気付けることが多いからです。実践している人も多いかもしれませんね。そうした使い方も、ぜひ試してみてください。

自分で実装する浮動小数点数値の加算（かわさき）

かわさきしんじ

かわさきしんじ

　大学生時代にIT系出版社でアルバイトを始めて、そのまま就職という典型的なコースをたどったダメ人間。退職しても何か他のことをできるでもなくそのままフリーランスの編集者にジョブチェンジ。そしてDeep Insider編集部に拾ってもらう。お酒とおつまみが大好き。通称「食ってみおじさん」。最近はすっかり「ダイエットおじさん」に変貌したのでした。

　いやー、夏ですね。少し歩くだけで、汗かきまくりです。ここのところ、朝5時半くらいからウォーキングを30分くらいするのが筆者のルーチンなのですが、それだけでもう汗ダラダラです。でも、やせません。たぶん、お酒飲み過ぎです。筋トレは普段、下半身を週に2回、上半身を週に2回ほどやっています。が、予定があるとそうはいかないこともあるんですよね。あ、予定ってのは酒飲みの予定です……。

　唐突に始まりますが、Pythonクイズの『「1.0 + 2.0 == 3.0」は期待通りにTrueになるはず？　その理由は分かる？』の最後で、「HPかわさき」こと筆者はこんなことを言っていました。

　ホントは2つの浮動小数点数値を与えると、それらをビット列に変換して、ビットごとの加算を行って、その結果をまた浮動小数点数値に戻して……なんてところまでやろう……（以下略）

　今回の編集後記では、実際に2つの浮動小数点数値を渡すとそれらを加算した結果を返す関数を定義してみることにしました。その前にIEEE 754で定められている浮動小数点数値についてカンタンにまとめておきましょう。

　ここでは64ビット長（倍精度）の浮動小数点数値を対象とします。倍精度の浮動小数点数値は各ビットを次のように使っています。

　以下は概略を示したものです（てきとーに描いたので、それぞれのサイズ感が異なっていると思いますが、気にしないでください）。

64ビット長の浮動小数点数値の構造

　符号ビットは0か1の値を取り、その値の符号は「-1^{符号ビット}」で計算されます（0なら正、1なら負になります）。

　指数ビットは符号なしの2進整数として表現されますが、実際の浮動小数点数値の計算ではバイアスとして1023がマイナスされる点には注意してください。1023をマイナスすることで、指数部が負と正の両方の値を取れるようにしているわけです。

　また、指数ビットが全て0の場合と、全て1の場合は特殊な扱いとなっている点にも注意が必要です（前者は非正規化数や±0を表すのに、後者はNaNやInfを表すのに使われます）。このため、指数ビットが取れる値の範囲は1から2046となり、バイアスの1023をマイナスすると、-1022から1023が指数が取れる最小値、最大値になります。今回の実装では、指数部が全て0、全て1の場合については処理を省略しています（あくまでも原理を試すのが目標でした）。

　例えば、指数ビットの値が1024なら、指数部の値は1024−1023＝1になります。つまり全体としては「-1^{符号ビット}×仮数ビットが表す値×2^1024-1023=1」という値を表します。

　仮数部は「1.fraction」のように常に「1」が先頭に来るような2進小数として表現されるものとされています。「1.fraction」として表現される仮数部全体を指して「significand」と呼び、「1.fraction」の「fraction」の部分をそのまま「fraction」と呼ぶことがあります。そして、52ビットの仮数ビットにはこのfractionが保存されます（先頭の「1」は多くの場合、常に「1」であり、仮数ビットには保存されません。「暗黙の1」と呼ぶこともあります）。ここでは、仮数部と仮数ビットと適当に使ってしまっていますが、仮数部は「1.fraction」を、仮数ビットは「fraction」を指していることには注意してください。

　以下はPythonクイズ本編で紹介した浮動小数点数のビット列への変換、ビット列から浮動小数点数値への変換を行う関数です（ビット列といっていますが、実際には0と1で構成される文字列です）。

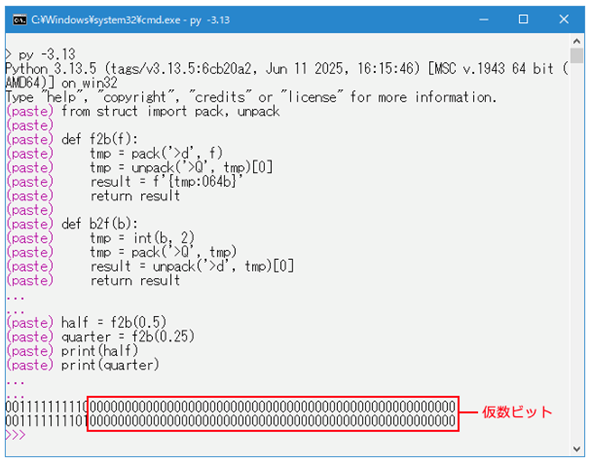
　ここで0.5と0.25をf2b関数に与えるとどうなるでしょうか。

　手元の処理系で実行した結果は次の通りです。赤い枠で囲んだ部分が仮数部（fraction）です。

0.5と0.25では仮数部（fraction）は同じ

　仮数部がどちらも全ビットが0である点に注目してください。0.5は2^-1で、0.25は2^-2です。2進の浮動小数点数値として表現するなら、0.5は-1⁰×1.0×2^-1と、0.25は-1⁰×1.0×2^-2と表現できます。仮数部の「1.0」のうちfractionだけを仮数ビットには保存するので、全ビットが0になっているということです。

　指数部についてはどうでしょう。0.5の方の指数部は「01111111110」＝1022で、0.25の方は「01111111101」＝1021となっています。ここからバイアスの1023をマイナスすると、0.5の指数部の値は1022−1023＝-1で、0.25の指数部の値は1021−1023＝-2となります。

　そういうわけで、上記のビット列が「0.5＝-1⁰×1.0×2^-1」「0.25＝-1⁰×1.0×2^-2」を正しく表現できていることが分かりました。

　ここまでが基本です。今回のテーマはこれらを加算する関数を定義することでした。ここでは2つの数値（浮動小数点数値）を与えると、その和を計算するadd_float関数を定義することにしましょう。

　add_float関数で浮動小数点数値を加算する際にはいろいろと考慮しなければならない点があります。

　2つの値をビット列に変換する点については説明は不要でしょう。両者から符号ビット、指数ビット、仮数ビットを取り出すのは以降の計算を簡単にするためです。

　2つの指数ビットの値が等しくなるようにするのはなぜでしょうか。上で見たように、0.5と0.25では仮数ビットの表現は同じで、指数ビットが異なっていました。以下はそれぞれを「1.fraction」形式で記述したものです（実際には仮数ビットには「1.fraction」の「1」は含まれないことに注意してください）。

「1.fraction」形式で0.5と0.25を表記

　ここで指数ビットが等しくなるように、ビット列を調整すると、次のようになることが分かります（ここでいう「ビット列の調整」とは仮数部の値を右にシフトして、結果、大きい方の指数ビットを用いて同じ値を表すように調整することです）。

指数ビットを等しくすると、ビット列の各ビットが相互に対応する桁の値になる

　つまり、指数ビットが等しくなるようにすることで、ビット列の各ビットが相互に対応する桁の値となるということです。これができたら、後は各ビットを足し合わせていけばよいだけです（キャリーの問題はありますが）。

　次に符号を考慮して、加算か減算を行います。ここで重要なのは、仮数は「2ⁿの和」の形で表現されている点です（2の補数表現が使われているわけではありません）。よって、2つの値の符号が同じであれば、2つの仮数を足し合わせます（その符号はどちらかの値の符号でよい）。2つの値の符号が違うのであれば、絶対値の大きい方から小さい方を減算します（その符号は絶対値が大きい方の符号になる）。簡単にいえば、1と-10の加算は「10から1を引いて9、符号はマイナスね」みたいな話です。

　単純に2つの仮数を足し合わせたり、絶対値が大きい方から小さい方を引いたりするだけでよいのは、両者の指数ビットが等しくなっているからである点にも注意してくださいね。

　そして、得られた結果を「1.fraction」形式の2進表記にします。これが正規化（normalize）と呼ばれる処理です。このときには、指数ビットの調整も必要になります。最後に、計算結果の符号、指数、仮数から計算結果全体を表すビット列を作成して、b2f関数に渡せば計算結果が浮動小数点数値として得られるというわけです。

　これを行うのが以下の関数群です。

　細かな説明はしませんが、adjust_exponent関数では2つの値の指数ビットが等しくなるようにどちらかの仮数ビットを調整します。基本的には指数ビットの値が大きい方に、小さい方を合わせます。0.5＝1×2^-1と0.25＝1×2^-2であれば、後者を0.1×2^-1とするようなイメージです。

　また、add_float関数で取り出す仮数ビットは文字列ですが、ここでは「int('1' + frac_a, 2)」のようにint関数を使って仮数ビットを整数に変換しています（'1'は「1.fraction」の「1」を表しています。また、frac_aはadd_floatに渡された2つの値のどちらかの仮数ビットです）。

　calc_sig関数では符号を考慮した仮数の計算をします。これは既に述べた通り、符号が同じなら両者の和を、符号が違えば両者の差を取るようにしています（上で述べたように仮数を整数値にしたことで、計算がシンプルに行えています）。

　normalize_frac関数では、仮数を「1.fraction」の形式にして、その「fraction」とその際に調整された指数ビットを返すようにしています。

　最後のadd_float関数では、2つの値を受け取り、上記の関数を呼び出して、最後に計算結果のビット列を組み立てて、b2f関数に渡し、その結果を返すようになっています。

　というわけで、これらの関数を使って実際に計算をしてみましょう。

　「0.5＋0.25」は「0.75」になりました。これは「1.0×2^-1＋1.0×2^-2」であり、「1.1×2^-1」です。「1.fraction」形式の「fraction」は「1」になるので、「print(c[12:])」では先頭に「1」があるということですね。

　では、Pythonクイズでやっていた「0.1＋0.2」がどうなるかを試してみましょう。ここでは小数点以下18桁の有効桁数で計算結果を示しています。また、Pythonの浮動小数点数値の加算結果も同時に示しておきましょう。

　微妙に誤差があります。これはadd_float関数の実装ではまるめ誤差の処理などをしていないからだと思われます。が、スタート地点としてはまあこんなものでしょう。興味のある方は、NaNやInfの対応、減算／乗算／除算の追加など、いろいろと試してみてくださいね。

「Deep Insider's Eye　一色＆かわさきの編集後記」