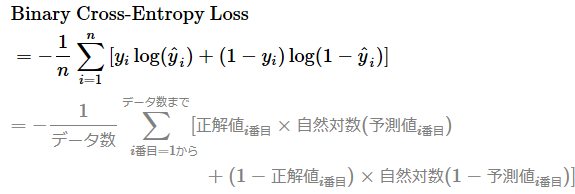「ロジスティック回帰」による分類をPythonで学ぼう:機械学習入門
「知識ゼロから学べる」をモットーにした機械学習入門連載の第5回。いよいよ今回から、「Yes/No」や「スパムかどうか」といった“分類”予測を扱います。これを実現する代表的な手法が「ロジスティック回帰」です。図を使って仕組みや考え方をやさしく学び、Pythonとscikit-learnでの実装も体験します。初めての人でも安心して取り組める内容です。
「この商品は売れるか/どうか?」「この顧客はサービスを解約しそうか/どうか?」―― こうしたYes/Noの判断(=分類)をデータから予測したい場面は、ビジネスや日常でたくさんありますよね? 今回は、このような際に役立つ、機械学習の代表的な手法であるロジスティック回帰による“分類”について学んでいきましょう。
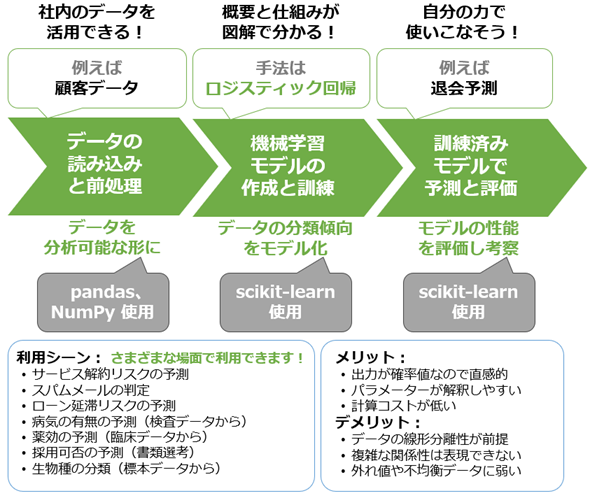
具体的には、ロジスティック回帰の概要から、その仕組み、そしてPythonプログラミングによるモデルの実装と評価まで取り組み、“分類”の基礎スキルを短時間で習得することを目指します(図1)。“分類”をマスターすると、これまで「経験や勘に頼っていた判断」を「データの裏付けがある判断」に変えることができ、ビジネスの意思決定にも大いに役立ちます。
これまでの連載では、第3回で線形回帰について、第4回でラッソ回帰とリッジ回帰について、つまり“数値”を予測する「回帰」の手法を学んできました。今回からは新たなテーマに入り、“カテゴリー”を予測する「分類」の手法を学んでいきます。次回以降では、決定木、ランダムフォレスト、サポートベクターマシン、k-近傍法と続くのでお楽しみに!
なお今回も、大事なエッセンスにフォーカスし、過去記事との共通部分はできるだけ省略しています。ただし、ロジスティック回帰は線形回帰よりも少し複雑なため、仕組みの説明は約1.5倍ほどになります。一方、プログラミングはこれまでの知識の応用なので、短時間で読めるはずです。よって、記事全体のボリューム感は線形回帰と同じくらいだと想定しています。
今回で学べること
ロジスティック回帰は、「Yesか/Noか」といった二値(=2クラス)の“分類”問題を解くための、基本的で実用性の高い手法です。例えば「このメールはスパムか/どうか?」といった問いに対し、データに基づく“予測”によって判断できます。機械学習における分類手法の中でも、まず習得しておきたい“必修スキル”と言えます。
図1に示した通り、今回のロジスティック回帰モデルも、Pythonライブラリ「scikit-learn」を使えば手軽に実装できます。本稿ではまず、ロジスティック回帰の基本的な概念や考え方を図を使って分かりやすく解説します。その後、実践で役立つ代表的な使用例に絞って、Pythonによる実装を体験していきます。
また、【発展】としてソフトマックス回帰と呼ばれる手法も簡単に紹介します。ロジスティック回帰が二値分類に用いられるのに対し、ソフトマックス回帰は3つ以上のクラスを扱う多クラス分類のための応用的な手法です。多項ロジスティック回帰(の一種)とも呼ばれる、この手法を習得すれば、より幅広い分類問題に対応できるようになります。
まとめると、今回は図2に示す内容を学ぶことができます。
それでは、まずはロジスティック回帰の概要紹介から始めていきます。
連載:
「機械学習は難しそう」と思っていませんか? 心配は要りません。この連載では、「知識ゼロから学べる」をモットーに、機械学習の基礎と各手法を図解と簡潔な説明で分かりやすく解説します。Pythonを使った実践演習もありますので、自分の手を動かすことで実用的なスキルを身に付けられます。
本連載では、具体的な機械学習の手法(例:線形回帰、決定木、k-meansなど)を解説しています。次回以降の新着記事を見逃さないように、ぜひ以下のメール通知の登録をお願いします。
何の役に立つ手法?
ロジスティック回帰(Logistic Regression)は、入力データと出力結果の関係を「S字型の曲線」(=ロジスティック関数、詳細は後述)でモデル化する手法です。一方、線形回帰モデルでは、「曲線」ではなく「直線」で関係を表現していました。この違いが特に重要なポイントです。
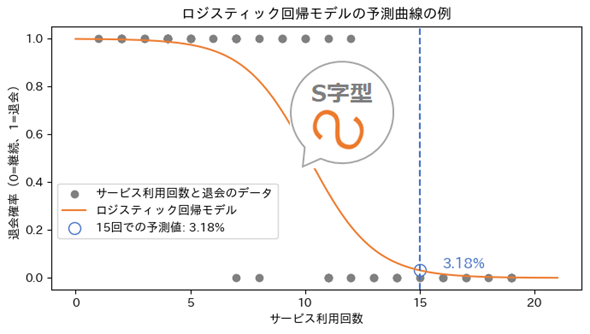
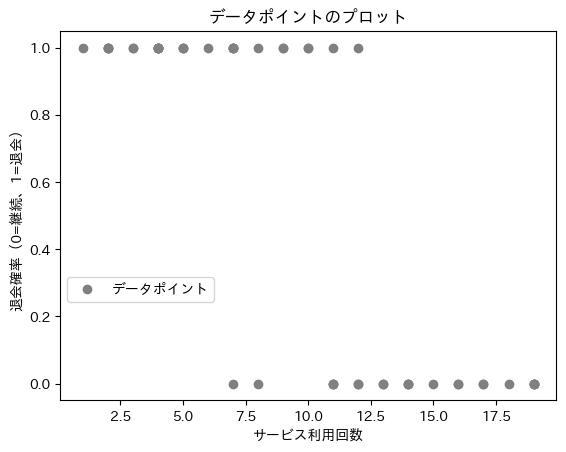
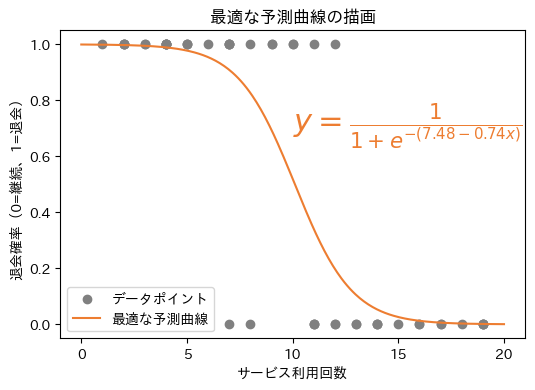
例えば図3は、入力データ(説明変数、特徴量)として「サービスの利用回数」を、出力結果(目的変数、ターゲット、ラベル/クラスラベル)として「退会した(1)/していない(0)」を持つ架空のデータから散布図を作成し、その上にロジスティック回帰モデルの予測曲線(S字カーブ)を引いた図です。
散布図の全ての点に“最も当てはまりのよい曲線”を引いています。これがロジスティック回帰の本質です。この曲線から、例えばサービス利用回数が15回の時は退会確率が3.18%ということ(=予測値)が読み取れますね(図3で青色で示した部分)。
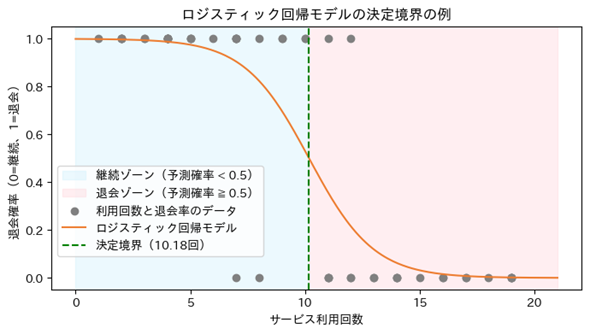
ただし、確率値のままでは「Yesか/Noか」という“分類”には使いづらいですよね。そこで、0.5未満なら「継続」、0.5以上なら「退会」、という基準(=閾値《しきいち、いきち》:threshold)を設けて、確率値を0(=No)か1(=Yes)かに離散化(discretization、つまり連続値を2つのカテゴリーに分割)します。それをグラフ化したのが図4です。
離散化の基準となる線(図4では緑色の点線)は、決定境界(Decision Boundary)と呼ばれます。図4のようにこの境界線によってグラフを分割すると、散布図のどの点が「継続=0」か/「退会=1」かを視覚的に把握しやすくなります。以上が、図で理解する「ロジスティック回帰による“分類”方法」です。
このようにして分類できれば、例えば以下のような場面で役立ちます。実際にロジスティック回帰は、さまざまな分野で幅広く使われています(冒頭の図1にも記載しています)。
- メールが「スパムか/どうか」の判定
- 顧客が「退会するか/どうか」の予測
- 商品の購入に「至るか/どうか」の判定
いずれも、曲線で表現された分類モデルによって「どちらかのカテゴリー(例:スパム/非スパム、退会/継続、購入/非購入)に属する確率を予測し、さらに決定境界で分類する」ことで実現されます。機械学習におけるロジスティック回帰は、このようにして“二値分類”の問題を解決できます。
特徴量が1つのモデル
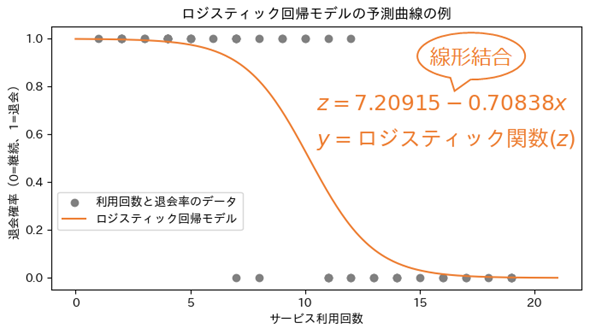
もちろん、図3(や図4)に描かれたS字型の曲線は、数式によって形が作られています。実はこの曲線も、線形回帰と同じように「xに数字を入れて、そこからyを計算する数式」で定義されています(その内容は後で詳しく見ます)。
まずは、図5にあるz=7.20915−0.70838xのような数式で、x(ここでは「サービス利用回数」)を使って途中の計算値zを求めます。この計算は、中学で学ぶ一次式(=直線の数式)なので簡単ですね。この計算の仕方は線形回帰と全く同じです。詳しくは後述します。
次に、このzを「S字型のカーブを描くロジスティック関数」に通すことで、最終的なyの値(ここでは「退会確率」)を算出します。言い換えると、「まずは直線で途中の値zを計算し、そのzを曲線に変換して確率値を求める」という、2ステップの構造になっているのです。
このようにロジスティック回帰は、線形回帰とは“兄弟のような関係”です。よってロジスティック回帰でも、直線が持つ「傾き」、つまり変数に「係(かか)る数(=かけ算する数)」は回帰係数(regression coefficient)と呼ばれます。切片(intercept)という用語もそのまま使われます。
回帰係数を求めることは回帰分析に相当すると言えますよね。……そんなわけで、“分類”のための手法なのに「ロジスティック“回帰”」という、ちょっと紛らわしい名前になっています(苦笑)。
特徴量が2つ以上のモデル
線形回帰モデルは、特徴量が1つなら「直線」、2つなら「平面」、3つ以上なら「超平面」で表現されました。一方、ロジスティック回帰モデルは少し異なり、特徴量が1つなら「S字型の曲線(Curve)」、2つなら「曲面(Surface)」、3つ以上では「超曲面(Hypersurface)」で表現されます(※なお、実際の“分類”は、既に説明した通り、その出力に閾値を設けた「決定境界」によって行われます)。
ただし、曲面や超曲面は図にしても直感的な理解が難しいため、本稿では特徴量が2つ以上のモデルの図示を省略します。イメージとしては、線形回帰の「回帰平面」が「曲面」に置き換わったようなものと考えるとよいでしょう。
ちなみに、線形回帰では、特徴量が1つのモデルを「単回帰」、2つ以上のモデルを「重回帰」と呼び分けていました。一方、ロジスティック回帰では、一般にそうした用語の区別は行われません。
以上で、「ロジスティック回帰が線形回帰を応用した手法であること」が分かってきたと思います。ただし、モデルのパラメーター(例えば先ほどの数式に出てきた切片7.20915や係数−0.70838)を決定する仕組みは、線形回帰の計算方法「最小二乗法」とは異なります。次に、その仕組みを見ていきましょう。
どんな仕組み?
データに最もフィットするロジスティック回帰モデル(S字型の予測曲線/曲面/超曲面)の各パラメーターを見つけるためには、一般的に「最尤(さいゆう)推定」(=最尤法)と呼ばれる計算方法が用いられます。以下で、その仕組みをできるだけ数式ではなく図解を中心に説明していきます。
ステップ1: 訓練セットを準備
まずは訓練用のデータセットが必要です。以下の説明では、先ほどの例(図3〜5)と同じデータを使うことにします(図6)。このデータには、特徴量(x)として「サービス利用回数」が、ターゲット(y)として「継続(0)/退会(1)」のラベルが含まれています。
今回は、図6に描かれた全ての点に“最も当てはまりがよい曲線”を引きたいですね。そこで、まずは適当に仮の予測曲線を引いてみます。
ステップ2: 仮の予測曲線を設定
前掲の図5でも説明したように、ロジスティック回帰の予測曲線を描くには、
- (1)途中の値zを求める: ※この数式でいったん「直線」になる
- (2)そのzから確率値(0.0〜1.0)を求める: ※この数式によって「S字型の曲線」に変わる
という、2ステップの計算が必要です。
(1)線形結合
まず(1)の計算には、線形結合(linear combination)や重み付き線形和(weighted linear sum)と呼ばれる方法を用います。具体的には、切片をパラメーターβ0、サービス利用回数(x)に対する係数(直線の傾き)をパラメーターβ1と置くと、数式は以下のようになります(※線形回帰と同じ式)。
ところで、次に示す数式の中に、数学記号のネイピア数e(=オイラー数、自然対数の底)が出てきますが、数式にeを使うと「微分をしやすい(=傾きを計算しやすい)」、つまり「パラメーター最適化の計算がしやすい」というメリットがあるために採用されている、と知っておけば、仕組みを理解するには十分です。
(2)ロジスティック関数
次に(2)の計算には、ロジスティック関数(Logistic function、厳密には標準ロジスティック関数)と呼ばれる方法を用います。具体的には以下の数式により、先ほど計算した線形結合の結果(z)に対する予測確率(y)を求める計算になります。
この関数により、線形結合による「直線」は、「S字型の曲線」に変換されます(図7)。S字型(=シグモイド)になることから、ロジスティック関数はシグモイド関数(Sigmoid function)とも呼ばれます(※ちなみに、ニューラルネットワークではその呼び方が主流です)。
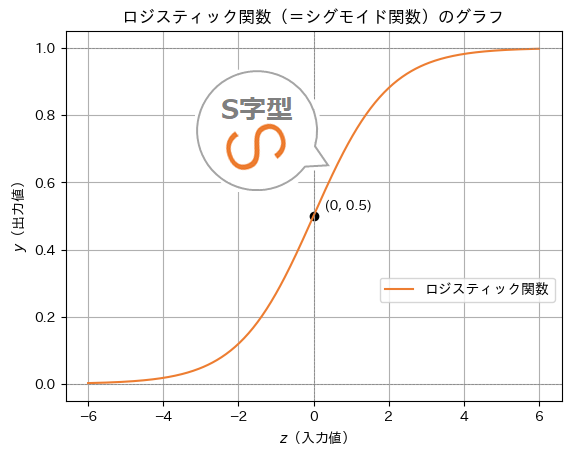
図7 「直線」を「S字型の曲線」に変換するためのロジスティック関数
※カーブの形が「S」の字であることに注目! なお、前掲の図3が「S」字を上下反転させた形だったのは、係数がマイナスであったことにより、曲線グラフの上下の向きが反転していたためです。
それではなぜ、「直線」を「S字型の曲線」に変えるのでしょうか? 図7のグラフを見ながら、少し考えてみてください。
理由は、「直線」だと縦軸の値の範囲が無限(―∞〜∞)になってしまうからです。一方、「S字型の曲線」なら縦軸の値の範囲は0.0〜1.0に収まります。つまり0〜100%の確率(probability)として扱えるのです。確率なら「継続か/退会か」のような判別にピッタリですね。
要するに、「実数値を確率値に変換すること」がロジスティック関数の役割です。
仮の予測曲線
さて、以上の2つの数式を組み合わせると、次のような数式にまとめられます。以下ではこの形で使っていくことにします。
今回は図解で説明するために、各パラメーターに対する仮の初期値を設定します。この初期値はあくまで「仮」なので、好きに決めて構いません。ここではβ0の初期値は−5.0、β1の初期値を0.5としましょう。
これにより、
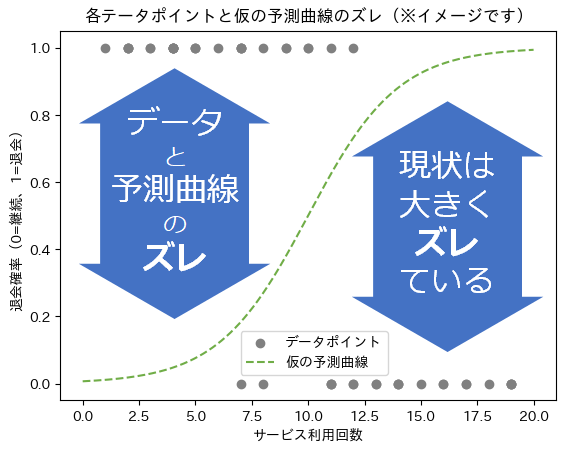
という数式の予測曲線になります。図8に、この曲線を描いてみました。
図8では「仮の予測曲線が、実際のデータからどれくらいズレているか」に注目してください。この場合のズレとは、「各データポイント」と「仮の予測曲線(=ロジスティック回帰モデル)」の間の距離のようなものです。厳密には距離ではないのですが(詳細後述)、図8には参考イメージとして「ズレの矢印」を描いてみました(この予測曲線だと、利用回数が少ないほど、退会しないことになってしまっています)。
デタラメな初期値だったので、データと曲線が全くフィットしていませんね。ロジスティック回帰では、これを最適な曲線に自動的に調整しようというわけです。
ステップ3: 正解と予測のズレの考え方
線形回帰では、正解値(=各データのターゲット)と予測値(=モデルの出力値)という実数値同士の引き算だけで、簡単に「距離」が計算できました。
一方、ロジスティック回帰では、正解値(=ここでは「継続(0)か/退会(1)か」の正解ラベル)と、予測値(=ここでは退会確率)の「ズレ」を計算しますが、これらの値は確率値(=%単位に加工された値)であるため、単純に引き算しても正しい「距離」にはなりません。
ワンホット表現
「えっ、継続(0)か/退会(1)か、も%単位の“確率”なの?」と思ったかもしれません。こういったカテゴリー値は、「継続」が何%か、「退会」が何%か?、という2項目に分けると、それぞれを“確率”として扱えます。
ちなみに、例えば「休会」が何%か、を加えるなどして3項目以上に増やすことも可能です(=多クラス分類の場合)。
例えば正解値が1なら、継続=0%、退会=100%になります。正解値が0なら、継続=100%、退会=0%ですね。パーセントを数値で表現すると0%=0.0、100%=1.0ですので、ターゲットとなる複数の項目のうち、正解の1項目だけが1で、残り全ての項目は0になります。
正解値を1つにまとめて数学的にベクトルで書くと、継続=[0, 1]や、退会=[1, 0]と書けます。このような書き方は、ワンホット(one-hot)表現と呼ばれます。また、このように変換することをワンホットエンコーディングと呼びます。
確率分布のズレ
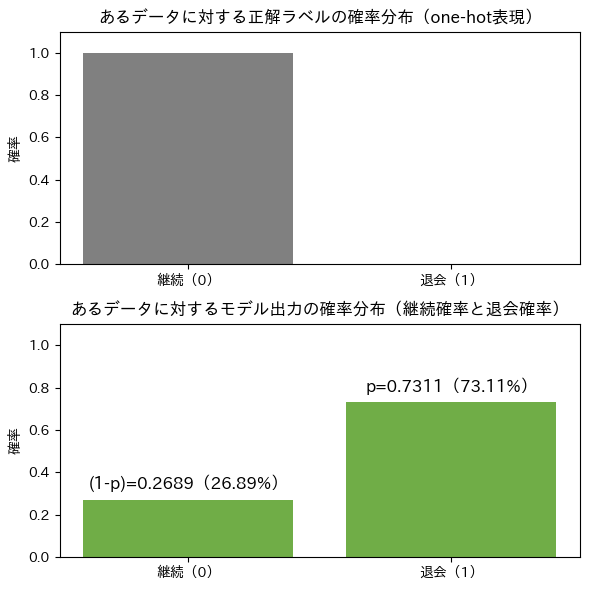
そして、[1, 0]や[0, 1]は確率分布と見なせます。図9は、あるデータポイントの正解値を「継続」と「退会」の2つの棒グラフで表現することで、確率分布のグラフとなっています。同様に、そのデータを入力した際のモデルによる予測値も確率分布として表現できます。
図9の下にあるp(確率:probabilityの“p”)は、「退会確率」を表します。逆に「継続確率」は、100%(=1.00)から退会確率(p)を引けばよいので、1−pになりますね(※これら2つの変数は、後述の数式で活用されます)。
このように考えることで、各データに対して「正解ラベルの確率分布」と「モデル出力の確率分布」のズレ(=不一致)を計算すればよくなります。その計算方法が、交差エントロピー(Cross-entropy、クロスエントロピー)という関数です。「交差エントロピー損失(Loss)」や「交差エントロピー誤差(Error)」とも呼ばれます。
線形回帰では、「残差」と呼ばれるズレの合計値を計算するためにRSS(残差の二乗和)という関数を使いましたが、交差エントロピーはそのロジスティック回帰版だと考えると分かりやすいでしょう。
ステップ4: 交差エントロピーの計算
交差エントロピーは、確率分布のズレを自然対数を用いて数値化します。その数式は、タスクが「二値分類(Binary Classification)」か「多クラス分類(Multi-class Classification)」かで少し異なります。ここでは二値分類タスクを解いているため、二値分類用の数式を紹介します。多クラス分類用はあとで紹介します。
二値分類用の交差エントロピー
以下の数式では、nはデータ数(iはその何番目か)、logは自然対数(=ln、つまりネイピア数eを底とする対数)、Σは総和を表します。この数式が「何をしているか」の意味はあとで説明するので、数式はざっと見るだけで構いません。
この数式は+の箇所で左右に分かれます。+の左側ではp(ここでは退会確率)のズレを、右側では1−p(ここでは継続確率)のズレを計算しています。左右どちらも「正解が退会(1)か/継続(0)か」に応じて、正解と予測のズレを計算する内容になっていますので、左側だけ説明します。
左側の正解値i番目 × 自然対数(予測値i番目)という計算に注目してください。正解値i番目が0の場合、0に何を掛け算しても結果は0になりますよね。
正解値i番目が1の場合、予測値i番目が1.0なら、自然対数の計算に基づき、その結果は0です。同様の計算で、0.5なら−0.7、0.1なら−2.3となります。つまり、予測が間違っているほど(=ズレが大きくなるほど)、結果の数値がマイナス方向に大きくなります。ちなみに、数式の先頭に−(マイナス)が付いているのは、マイナス×マイナス方向で「プラスの値」にするためです。
なお、予測値i番目が0.0もしくは1.0の場合、数学的に計算が不可能な「log(0)の計算」が発生するため避けなければなりません。そのため、scikit-learnなどのライブラリでは、予測値i番目が0.0や1.0にならないように、非常に小さな値(epsilon)を用いて、数値を[epsilon, 1−epsilon]の範囲に制限(clip)しています。これにより、log()関数の入力が常に有効な範囲に収まるため、安全に計算できるようになっています。
このように計算した左側(p)と右側(1−p)、2クラス分のズレを足し算した上で、全データ分を合計してデータ数で割ることで平均している、というのが「二値分類用の交差エントロピーの数式」の意味です。
これにより「ズレの平均値」が求まります(単に「損失」や「誤差」とも呼ばれます)。その損失値が小さいほど「データに当てはまりのよい(=フィットする)曲線」であることを表します。つまりロジスティック回帰モデルの予測精度が高いということです。
なお、予測値i番目の部分には、前述したロジスティック関数(数式を以下に再掲)が代入されます。ただし、実際に代入した数式は少し複雑になり難しい気分になるので(苦笑)、あえて省略します。
このロジスティック関数の出力を使った「交差エントロピー」の数式を使って、パラメーターβ0(切片)やβ1(サービス利用回数に対する係数)を求める方法を見ていきましょう。ロジスティック回帰の目標は、ズレ(=交差エントロピー)ができるだけ小さくなるような、最適なパラメーターを見つけることです。
ステップ5: 交差エントロピーの最小化
最適なパラメーターの求め方は、基本的には線形回帰のRSS(残差の二乗和)の最小化と同じ考え方です。具体的には、図10に示す曲線の谷底を見つけるイメージです。
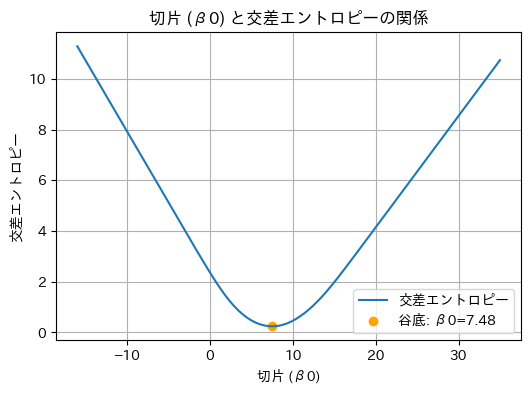
図10 仕組みの理解: 交差エントロピーで描く曲線(切片)の谷底を見付ける
パラメーターβ0(切片)の谷底を可視化しています。この曲線は、ロジスティック回帰モデルのパラメーターβ1(サービス利用回数に対する係数)を(実際に計算した最適値である)−0.74で固定して、パラメーターβ0(切片)にさまざまな値を入力してみた場合の、交差エントロピーの値をグラフ化したものです。
一番谷底の部分が、交差エントロピーの計算値が最も小さくなる「最適なパラメーター」です(=交差エントロピーの最小化)。
図10を下から上に見ると、「ズレの程度」(=交差エントロピー)がどれだけ大きいかが分かります。「ズレ(=不一致)」の真逆の概念は「一致」なので、逆の視点で上から下に見ると、「一致の程度」がどれだけ大きいかが分かりますよね。
この「一致の程度」は、「尤(もっと)もらしさ」という意味の尤度(ゆうど、Likelihood)を変換した数値です。「交差エントロピーの最小化」=「尤度の最大化」となるので、ロジスティック回帰におけるパラメーター推定の手法は「最尤推定」と呼ばれるのです。最尤推定については、あらためて後述のコラムで触れます。
ロジスティック回帰の場合、線形回帰のように最適なパラメーターを「数学の公式を使って一発で求める」(=解析的に解く)という方法が使えません。ロジスティック関数という非線形の変換が加わったため、曲線や曲面は山や谷が幾つもあるような形で波打っており、谷底を一発で計算すると局所的な谷底(=局所解)に嵌(は)まって間違った値になる可能性があるからです。
勾配降下法
ロジスティック回帰では、データごとに「曲線に対する接線の傾き」(=勾配:Gradientと呼ばれる)を計算して蓄積し、その勾配の合計から谷底の場所(=最適解)を探っていきます。勾配とは「坂道」のことで、つまりボールを投げて坂道を転がすイメージです(図11)。この最適化手法は、勾配降下法(Gradient Descent)と呼ばれます。
勾配降下法には、データ全体を使うバッチ勾配降下法や、ある程度のまとまりごとのデータを使うミニバッチ勾配降下法などがあります。ニューラルネットワークと同じなので(参考記事)、ここでは詳細を割愛します。
勾配降下法は、最適化アルゴリズムの一つに過ぎません。scikit-learnなどのライブラリでは、ロジスティック回帰で任意の最適化アルゴリズムを選択できます。いずれを使う場合も、最適なパラメーターβ0(切片)やβ1(サービス利用回数に対する係数)が求まります。
最適化アルゴリズムでは、「訓練(学習)を何回繰り返すか」を意味するイテレーション数(iteration)を決めて、その回数だけ谷底を探して最適化の度合いを高めることができます。また、「1回のイテレーションで学ぶスピード」を意味する学習率(learning-rate)を決める場合もありますが、scikit-learnでロジスティック回帰する場合は内部的に自動調整されるため、通常は指定できません。
図11は、勾配降下法により最小化が進む様子のイメージを示したものです。基本的に、最初はボールが谷底に向けて坂の急勾配を大きく転がり落ち、谷底に近づき徐々に坂の勾配が緩やかになるにつれてゆっくりと転がるようになっていき、最終的に谷の底(最小値)にたどり着くという流れです。
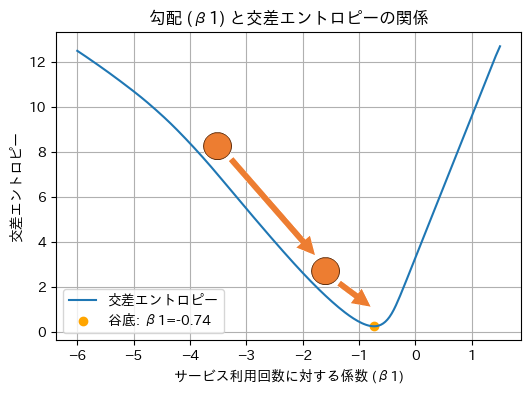
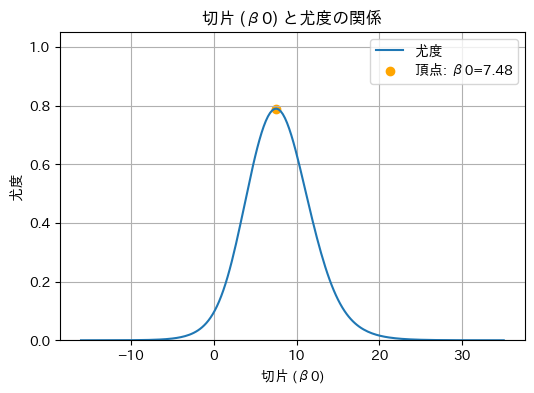
図11 仕組みの理解: 交差エントロピーで描く曲線(サービス利用回数に対する係数)の谷底を見付ける
パラメーターβ1(サービス利用回数に対する係数)の谷底を可視化しています。この曲線は、ロジスティック回帰モデルのパラメーターβ0(切片)を(実際に計算した最適値である)7.48で固定して、パラメーターβ1(サービス利用回数に対する係数)にさまざまな値を入力してみた場合の、交差エントロピーの値をグラフ化したものです。
このようにして各パラメーターの最適値を求めると、手元での計算例ではβ0は7.48、β1は−0.74と求まりました。前掲の図5と少しパラメーター値が異なりますが、これは使用した最適化アルゴリズムが異なるからです(※図5ではscikit-learnのデフォルトを使いましたが、ここでは勾配降下法で手動計算しました。参考:サンプルノートブック)。パラメーター値は、最適化アルゴリズムに何を使うかで変わってくるので注意してください。
ステップ6: 最適な予測曲線の決定
以上で、交差エントロピーが最小となる最適なパラメーターβ0とβ1が計算できたので、これらを用いて最終的なロジスティック回帰モデル(ここでは予測曲線)を決定します。まず線形結合の数式は以下のようになります。
このzをロジスティック関数に代入すると、以下の数式になります。
この数式の予測曲線を散布図上に描画すると図12のようになります。
以上のように最尤推定は、訓練セットに最も適したロジスティック回帰モデル(予測曲線/平面/超平面)を見つけるための計算方法というわけです。
【コラム】最尤推定と交差エントロピーの関係
先ほども説明したように、「ズレの程度を最小化すること」は「一致の程度(=尤度)を最大化すること」と同じ意味になります。ロジスティック回帰の最適化手法は、この「尤度の最大化」の視点から「最尤推定(Maximum Likelihood Estimation:MLE)」と呼ばれます。
考え方はシンプルで、「現在のモデル(予測曲線)が、訓練セットをどれだけもっともらしく説明できるか(=尤度)を最大にしよう」というものです。山型のグラフを思い浮かべてください(図13)。この山の頂上が「もっともらしさ(尤度)が最大」となるパラメーター値(の組み合わせ)です。
一方、交差エントロピーは「ズレを最小にしよう」という関数ですが、その中身(数式)は「負の対数尤度」そのものです。先頭にマイナスが付いているため、グラフの形が逆さ(山型→谷型)になって見えるだけなのです(つまり図10は、「この図13を逆さにして少し変形させたもの」とも言えます)。
「交差エントロピーを最小化すること」と「尤度を最大化すること」は、数学的には全く同じ意味です。視点が違うだけなので、「最尤推定? 難しそう」と構える必要はありません。
以上でロジスティック回帰モデルの各パラメーターを決定する仕組みを理解しました。続いて実践として、scikit-learnによるプログラミングを体験してみましょう。
体験してみよう
scikit-learnには、ロジスティック回帰モデルを構築できるLogisticRegressionクラス(sklearn.linear_modelモジュール)があります。
LogisticRegressionクラスの使い方
リスト1がその使い方です。線形回帰とほぼ同じなので、fit()メソッドまでの説明は割愛します。残り2行のメソッド呼び出しでは、訓練されたロジスティック回帰モデルを使って、予測の「確率値」と「最終的な予測結果(0か1の出力値)」を取得しています。
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(<特徴量:X>, <ターゲット:y>)
model.predict_proba(<新しいデータ>) # 予測値(=確率値)を出力
model.predict(<新しいデータ>) # 予測結果(=0か1か)を出力
predict_proba()メソッドでは、予測値として「確率値」(例:退会確率)が取得できます。が、この確率値が0.5以下なら0(例:継続)、0.5を超えるなら1(例:退会)のように、最終的なクラスラベル(0か1か)を決定したいですよね。こうした離散化された予測結果を取得したい場合には、predict()メソッドを使います。
もちろんLogisticRegressionクラスには、これら以外にもさまざまな機能が備わっています。詳しくは公式ページをご参照ください。
それでは、このクラスを使って実際にロジスティック回帰モデルを作成し、二値分類を行ってみましょう。
ノートブックの利用について
本連載は、第1回で説明したように、無料のクラウド環境「Google Colab」の利用を前提としています。基本的には、Colabで新規ノートブックを作って、以降で説明するコードを入力しながら実行結果を自分の目で確かめてください。既に入力済みのノートブックを使いたい場合は、こちらのサンプルノートブックをご利用ください。
実際に使ってみよう: データセットの読み込み
まずはデータセットを準備します。今回は、scikit-learnから読み込める「Wine(ワイン)データセット」を使います。入力データとなる特徴量には、下記の13項目があります。いずれも数値変数(実数値)であり、カテゴリカル変数(カテゴリー値)は含まれていません。
- alcohol: アルコール度数
- malic_acid: リンゴ酸
- ash: 灰分(かいぶん)
- alcalinity_of_ash: 灰分のアルカリ度
- magnesium: マグネシウム
- total_phenols: 全フェノール含量
- flavanoids: フラボノイド
- nonflavanoid_phenols: 非フラボノイドフェノール
- proanthocyanins: プロアントシアニン
- color_intensity: 色の濃さ
- hue: 色相
- od280/od315_of_diluted_wines: 希釈ワイン溶液のOD280/OD315(280nmと315nmの吸光度の比)
- proline: プロリン
出力結果となるターゲットは以下の通りです。これらは、3種類の異なる品種から作られた「ワインの種類」を表すクラスラベル(正解値)のうち、3つ目をカットして2種類にすることで、便宜的に二値分類用のデータセットとして応用したものです。
- クラス1: ブドウ品種「1」のワインで、値は「0」(59件)
- クラス2: ブドウ品種「2」のワインで、値は「1」(71件)
- (※二値分類タスクにするため「クラス3」はカットしました)
Wineデータセットについてより詳しく知りたい場合は、こちらの記事を参照してください。
このデータセットを読み込むには、sklearn.datasets.load_wine()関数を呼び出すだけです。訓練セットとテストセットに分割するまでのコードを以下のリスト2に示します。
from sklearn.datasets import load_wine
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# データセットの読み込み
wine = load_wine()
# 特徴量とターゲットの取得
X = wine.data
y = wine.target
# クラス1(0)とクラス2(1)のデータだけに絞り込む
mask = (y == 0) | (y == 1)
X = X[mask]
y = y[mask]
# データの標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 訓練セットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.1, random_state=0)
print(f'訓練セットのサイズ: {X_train.shape}') # 例: 訓練セットのサイズ: (117, 13)
print(f'テストセットのサイズ: {X_test.shape}') # 例: テストセットのサイズ: (13, 13)
なお、特徴量間のスケールが異なるため、前処理として各特徴量を標準化(=平均を「0」に、標準偏差を「1」のスケールに変換)しています。
実際に使ってみよう: 機械学習モデルの訓練
次に、いよいよLogisticRegressionクラス(sklearn.linear_modelモジュール)を使ってロジスティック回帰モデルを作成し、訓練します。リスト3はそのコード例です。
from sklearn.linear_model import LogisticRegression
# ロジスティック回帰モデルの訓練
model = LogisticRegression(solver='lbfgs')
model.fit(X_train, y_train)
print('係数:', model.coef_)
print('切片:', model.intercept_)
# 係数: [[-1.50497653 -0.53548103 -0.90018867 1.00264039 -0.31198706 -0.09362577
# -0.28866105 0.2635515 0.25998733 -0.74083219 -0.00681288 -0.62169609
# -1.85070478]]
# 切片: [0.2751988]
LogisticRegressionクラスのsolverパラメーターには、最適化アルゴリズム(solver:ソルバー)を指定できます。リスト3では、デフォルト値と同じ'lbfgs'を指定しました(省略も可能ですが、説明のため明示しています)。
主な選択肢は以下の通りです。各アルゴリズムの詳細な仕組みには立ち入りませんので、ここでは名称と使い分けの目安を押さえておきましょう。
- 'lbfgs'(デフォルト): 「準ニュートン法」の一種で、「BFGS法」に基づくソルバー。中〜大規模データセット向き。高速で安定しており、分類タスクでは多くの場合これで十分。
- 'liblinear': 「LIBLINEAR」ライブラリを利用したソルバー。小規模データセットでは高速。多クラス分類では別のソルバーの方が基本的に良い(※クラスごとに分類を行う「1対その他(one-vs-rest)」方式のため、複数クラスを一括で分類できる他のソルバーより非効率になりやすい)。
- 'newton-cg': 「ニュートン法」の一種で、「共役勾配法(conjugate gradient)」を用いるソルバー。中〜大規模データセット向きだが、'lbfgs'より遅くなることもある。
- 'newton-cholesky': 「ニュートン法」の一種で、「コレスキー(cholesky)分解」を用いるソルバー。大規模データセットのうち、特にサンプル数(=データの行数)が「特徴量数×クラス数」を大きく上回る場合に向く。
- 'sag': 確率的勾配降下法(SGD)を改良した「確率的平均勾配法(SAG)」を用いるソルバー。小規模データでは遅くなりやすいが、非常に大規模なデータセットでは高速に動作する。特徴量は事前にスケーリング(標準化など)しておくと収束(=最適化)が速くなる。
- 'saga': 「確率的平均勾配法(SAG)」をさらに改良したソルバー。非常に大規模なデータセットに強い。'sag'と同様、特徴量のスケーリングが重要。
※'sag'や'saga'の名前にある「g」(Gradient)は、上記の「どんな仕組み?」の説明で扱った「勾配降下法(GD:Gradient Descent)」の一種であることを示しています。
最適化アルゴリズムの数式や詳しい仕組みを知らなくても、上記の指針を参考にソルバーを選べば実用上は十分です。モデルの予測精度を高める際は、異なるソルバーを1つずつ試して比較してみてもよいでしょう。迷ったときは、まず'lbfgs'を使えば、多くの場合うまくいきます。
加えて、リスト3の最後で出力したmodel.coef_(係数)とmodel.intercept_(切片)から、モデルの内部状態を数値で確認できますね。なお、この例では、係数の数が13個と多いため、高次元のグラフとなり図示できませんが、係数が1個であれば、前掲の「図3 ロジスティック回帰モデルの予測曲線の例」のように図示できます。
実際に使ってみよう: 訓練済みモデルによる予測
次に、リスト4はそのモデルを使ってテストセットから「ワインのクラス(0か1か)」を予測するコード例です。
# テストセットを用いて分類予測(予測結果と確率値の取得)
y_pred = model.predict(X_test)
y_proba = model.predict_proba(X_test)
# 先頭5件の予測結果と、その予測確率値を表示
print(f'実際のクラス(先頭5件):{y_test[:5]}')
print(f'予測結果(先頭5件):{y_pred[:5]}')
print('---')
print(f'予測確率値(先頭5件):\n{y_proba[:5]}')
# 実際のクラス(先頭5件):[0 1 1 1 1]
# 予測結果(先頭5件):[0 1 1 1 1]
# ---
# 予測確率値(先頭5件):
# [[0.99578134 0.00421866]
# [0.00122679 0.99877321]
# [0.0013692 0.9986308 ]
# [0.02719697 0.97280303]
# [0.00682272 0.99317728]]
※「予測確率値」は、各行が[クラス0の確率, クラス1の確率]を表します。例えば1行目の[0.99578134, 0.00421866]は、「クラス0=99.578134%」「クラス1=0.421866%」という意味で、合計は100%(=1.0)になります。
予測結果(=predict()メソッドで得られるクラスラベル)と、実際のクラス(=テストセットの正解ラベル)を比較できるように出力しています。先頭の5件は全て正解しており、正解率は100%でした。それでは、テストセット全体での正解率はどの程度なのでしょうか? 評価してみましょう。
モデルの評価と考察
リスト5は、訓練済みのロジスティック回帰モデルを使って、テストセット全体に対する分類モデルの性能を評価するコード例です。分類タスクでは「正解率」がよく使われますが、このコードでは「適合率」「再現率」「F1スコア」など、正解率とは異なる観点の評価指標も併せてチェックしています(これらの評価指標は後ほど簡単に説明します)。
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
# 予測結果(y_pred)と正解ラベル(y_test)を比較して、各評価指標を算出
acc = accuracy_score(y_test, y_pred)
prec = precision_score(y_test, y_pred)
rec = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
# 結果を出力
print(f'正解率(Accuracy): {acc:.2f}')
print(f'適合率(Precision): {prec:.2f}')
print(f'再現率(Recall): {rec:.2f}')
print(f'F1スコア(F1 Score): {f1:.2f}')
# 正解率(Accuracy): 1.00
# 適合率(Precision): 1.00
# 再現率(Recall): 1.00
# F1スコア(F1 Score): 1.00
リスト5では、テストセット全体でも「全ての評価指標で1.00(=100%)の性能であること」が確認できました。非常に優秀な分類モデルですね。もしくは、今回のデータセットでの分類タスクは、簡単過ぎたのかもしれません。
分類モデルの評価では、「正解率だけを見て安心しない」ことが大切です。
例えば、正解ラベルが1(=陽性:Positive)であるデータが100件中わずか2件しかない場合、全てを0(=陰性:Negative)と予測するだけで、正解率は98%になります。見かけ上は高性能に見えても、重要なクラス(この場合は陽性)を一度も検出できない、非常に偏ったモデルになっている可能性があるのです。
もし陽性が「病気あり」を表すなら、全てを「病気なし」と判定するのは、危険なモデルですよね。このような偏りを見逃さないために、正解率だけでなく、再現率、適合率、F1スコアなど複数の評価指標を併せて確認するのがお勧めです。
それでは、リスト5で使った評価指標について簡単にまとめます。初学者が押さえておきたい重要な指標ですが、数式や計算方法は省略するので、必要に応じて各項目のリンク先を参照してください。それぞれ少しずつ違っていて覚えにくいかもしれませんが、使うたびに以下の内容を何度も見返してみるとよいでしょう。
- 正解率(Accuracy):
- 「全ての予測結果のうち、どれくらい正解したか」の割合を示す評価指標。最も基本的な指標であり、分類タスクでは常に使われる。
- 評価値: 値の範囲は0.0(=0%)〜1.0(=100%)で、大きいほど良い。
- コード: sklearn.metricsモジュールのaccuracy_score()関数で計算できる。
- 注意点: 先ほど述べたように、クラスに偏りがあると実際よりも高く見えることがあるので、他の指標も併用するのが望ましい。
- 適合率(Precision):
- 「陽性(この例ではクラス2)と予測した中で、本当に陽性(クラス2)だった割合」を示す評価指標。つまり「陽性と予測した結果が、どれくらい信頼できるか」を表す指標であり、誤って陽性と判定するケース(False Positive:偽陽性)を減らしたい(=ムダな陽性判定を減らしたい)場面で使われる。
- 評価値: 値の範囲は0.0(=0%)〜1.0(=100%)で、大きいほど良い。
- コード: sklearn.metricsモジュールのprecision_score()関数で計算できる。
- 注意点: 陽性と予測する件数が少な過ぎると、評価が不安定になりやすい。
- 再現率(Recall):
- 「実際に陽性(この例ではクラス2)だった中で、正しく陽性(クラス2)と予測できた割合」を示す評価指標。つまり「本来検出すべき陽性を、どれくらい見逃さずに予測できたか」を表す指標であり、誤って陰性と判定するケース(False Negative:偽陰性)を減らしたい(=見逃しを防ぎたい)場面で使われる。
- 評価値: 値の範囲は0.0(=0%)〜1.0(=100%)で、大きいほど良い。
- コード: sklearn.metricsモジュールのrecall_score()関数で計算できる。
- 注意点: 適合率とトレードオフの関係にあるため、再現率だけが高くても「誤って陽性と判定する件数」(False Positive:偽陽性)が増え、過検出になっている可能性がある。
- F1スコア(F1 Score):
- 「適合率」と「再現率」の両方を考慮したバランスの良い評価指標で、2つの調和平均として計算される。どちらか一方が極端に低いとF1スコアも低くなるため、「どちらも大事にしたい」場面で使われる。
- 評価値: 値の範囲は0.0(=0%)〜1.0(=100%)で、大きいほど良い。
- コード: sklearn.metricsモジュールのf1_score()関数で計算できる。
- 注意点: どちらか一方が極端に低い場合は評価が偏るため、単独での使用は避け、「正解率」「適合率」「再現率」など複数の指標と併用するのが望ましい。
以上で、ロジスティック回帰による二値分類の基礎から実装方法までを学びました。次は【発展】として、これを多クラス分類に拡張した「ソフトマックス回帰(多項ロジスティック回帰)」を紹介します。少し疲れてきたかもしれませんが、ここまでの知識を応用すればスムーズに理解できます。ここで立ち止まるのはもったいないので、ぜひこの流れのまま最後まで学び切ってしまいましょう!
【発展】ソフトマックス回帰による多クラス分類
ここまで紹介してきたロジスティック回帰は、2クラスの分類に使われるため、「二項(binary)ロジスティック回帰」とも呼ばれます。これに対して、3クラス以上の多クラスを分類する手法は、「多項(multinomial)ロジスティック回帰」と呼ばれることがあります。
その代表的な手法が、ソフトマックス回帰(Softmax Regression)です。ロジスティック回帰と基本的な仕組みは同じですが、以下の2つの点だけが置き換わります。
- 確率分布を求める関数: ロジスティック関数 → ソフトマックス関数
- 確率分布間のズレ(損失)を測る関数: 二値分類用の交差エントロピー → 多クラス分類用の交差エントロピー
つまり、この2点を押さえるだけで、ソフトマックス回帰も理解できちゃうということ。ここでもう少し頑張る方が断然お得ですよね!
※ちなみに、現在のscikit-learnのLogisticRegressionクラスでは、多クラス分類を行うと自動的に「多項(multinomial)=ソフトマックス回帰」方式が適用されます。ただし、前述の最適化アルゴリズムでも触れたように、'liblinear'ソルバーを使う場合のみ、「1対その他(ovr:one-vs-rest)」方式になります。この方式では、各クラスについて個別に二項ロジスティック回帰を実行するため、ソフトマックス回帰よりも非効率になりやすい点に注意してください。
それでは、「置き換えられる関数」と「変わらない考え方」に注目しながら、ロジスティック回帰と同じ流れに沿って、ソフトマックス回帰の仕組みを解説していきます。なお、重複する部分は省略し、要点に絞って紹介します。
「仕組み」で置き換わる部分
ソフトマックス回帰の仕組みでも、まずは仮のモデルを作成します。このモデルは、線形結合とロジスティック関数を組み合わせた関数でした。その「ロジスティック関数」を「ソフトマックス関数」に置き換えます。
ソフトマックス関数
ロジスティック関数では、「クラス1(=0)」の逆が「クラス2(=1)」なので、1つの関数で2クラス分の確率を表現できました。でも3クラス以上では、そうはいきません。
ソフトマックス関数(Softmax function)では、クラスごとに確率を計算する必要があります。例えば3クラスなら、「クラス1(y1)」「クラス2(y2)」「クラス3(y3)」という3つの予測確率(yj)を求めます。※jはクラス番号(1〜3など)です。
その計算式、つまり各クラスに対する線形結合の結果(zj)から予測確率(yj)を求める数式は以下のようになります。※mはクラス数です。kはクラス番号(1〜3など)ですが、分母の総和(Σ)では全クラスを対象とするため、、kはjとは別のクラス番号として使っています。
再び、ネイピア数eが登場しましたね。これは、勾配(=微分)の計算をしやすくするためでした。
数式が分からなくても気にしなくて大丈夫です。ロジスティック関数と同じように、「クラスごとの確率を出している」――その意味さえつかめていればOKです。
次に、正解ラベル(=「クラス1か/2か/3か」)と、予測値(=各クラスの予測確率)の“ズレ”を計算します。正解ラベルは、ワンホット表現にすることで確率分布と見なせます。予測値も、クラスごとの予測確率(yj)をベクトルに全てまとめれば、確率分布になります。これで、2つの確率分布の“ズレ”が測れるようになりますね。
確率分布のズレ
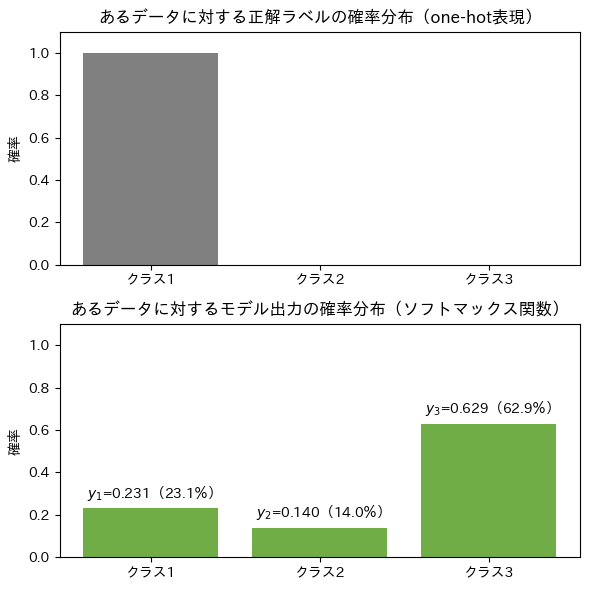
念のため、クラスが3つある場合の確率分布グラフを示します(図14)。ロジスティック回帰の場合とほぼ同じで、棒が1本増えただけです。
確率分布のズレは、交差エントロピーで数値化できました。しかし、その数式は、タスクが「二値分類」か「多クラス分類」かで少し異なるので、ここで多クラス分類用の数式を紹介します。
といっても、二値分類用と多クラス分類用で、やっていることは同じです。数式の見た目は違っても、「どちらもズレを測る式なんだ」と思っておけばOKです。
多クラス分類用のクロスエントロピー
以下の数式では、nはデータ数(iはその何番目か)、mはクラス数(kはそのクラス番号)、logは自然対数(=ln、底はネイピア数e)、Σは総和を表します。
二値分類用では、「+の箇所で左右に分かれる」と説明しました。多クラス分類では、これが「総和Σによって、クラスの数だけ+される」という説明になります。つまり、Σを+の繰り返しと見なせば、やっていることは二値分類と同じというわけです。
ズレが計算できたら、あとは勾配降下法などの最適化アルゴリズムを使って、最適なパラメーターを求めるだけです。これで、モデルは完成です。
以上がソフトマックス回帰の仕組みです。ロジスティック回帰をしっかり学んだからこそ、ソフトマックス回帰の理解はより簡単だったのではないでしょうか。
「体験(プログラミング)」で置き換わる部分
最後に、プログラミング上の違いについても触れておきましょう。といっても、ほとんど違いはありません。ポイントは次の2つだけです。
- (1)3つ以上のクラスへの対応
- (2)複数クラスの評価スコアに対応
全体的なコード内容は、ロジスティック回帰とほぼ同じになるため、全体の掲載は省略し、異なる部分だけを取り上げます。コードを実行してみたい方は、サンプルノートブックをご活用ください。
(1)3つ以上のクラスへの対応
ここでは、データセットに含まれる全てのクラスを使用します。先ほどは「クラス3」を除外していたので、あらためてターゲットとなる正解ラベルを以下に示しておきます。
- クラス1: ブドウ品種「1」で、値は「0」(59件)
- クラス2: ブドウ品種「2」で、値は「1」(71件)
- クラス3: ブドウ品種「3」で、値は「2」(48件)
前掲の「リスト2 Wineデータセットを読み込みコード例」では、maskによってわざわざ「クラス3」を除外していましたが、この処理が不要です。ここでは全てのクラスを使用するため、以下のように該当のコードをコメントアウトしてください。
# 絞り込むを解除して全てのクラスを使用
# mask = (y == 0) | (y == 1)
# X = X[mask]
# y = y[mask]
この変更だけで、モデルの訓練や予測のコードはそのまま使えます。
(2)複数クラスの評価スコアに対応
最後の評価用のコードもほぼそのまま使えますが、ほんの少しだけ書き加える必要があります。
というのも、多クラス分類の評価指標である適合率/再現率/F1スコアは、クラスごとに評価値(スコア)を計算するため、それらを平均(average)して最終的な評価値を求める必要があるからです。
この作業は簡単で、各評価関数にaverage='macro'という引数を追加するだけです。リスト7の太字部分を確認してください。
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
# 予測結果(y_pred)と正解ラベル(y_test)を比較して、各評価指標を算出
acc = accuracy_score(y_test, y_pred)
prec = precision_score(y_test, y_pred, average='macro')
rec = recall_score(y_test, y_pred, average='macro')
f1 = f1_score(y_test, y_pred, average='macro')
# 結果を出力
print(f'正解率(Accuracy): {acc:.2f}')
print(f'適合率(Precision): {prec:.2f}')
print(f'再現率(Recall): {rec:.2f}')
print(f'F1スコア(F1 Score): {f1:.2f}')
# 正解率(Accuracy): 1.00
# 適合率(Precision): 1.00
# 再現率(Recall): 1.00
# F1スコア(F1 Score): 1.00
ちなみに正解率(Accuracy)は、もともと全クラスをまとめて評価する指標なので、average='macro'の指定は不要です(そもそも指定できません)。
適合率/再現率/F1スコアを計算する関数の引数averageには、幾つかの指定値があります。それぞれの意味や使い分け指針、メリットとデメリットを以下に簡潔にまとめます。
- 'macro': マクロ平均。クラスごとの評価値を単純に平均する方法。各クラスを同等に扱うため、各クラスのデータ数に偏りがあっても、少数派クラスを軽視したくない場合に適している。
- 'weighted': 加重平均。クラスごとの評価値に、そのクラスのデータ数を重みとして掛けて平均する方法。各クラスのデータ数に偏りがある場合でも、実態に近いバランスでスコアを算出できる。実際のデータ分布を評価に反映したいときに有効。ただし、多数派クラスの影響は大きくなる。
- 'micro': マイクロ平均。全クラスで合算してから評価値を計算する方法。クラスの区別をしないため、正解率と同じ値になることもある。多数派クラスに大きく引っ張られるため、クラスごとにデータ数が大きく不均衡である場面では注意が必要。マクロ平均と比べることで、モデルが多数派クラスに偏っていないかどうかを確認するのにも役立つ。
通常は、リスト7のようにaverage='macro'を指定するのが無難です。ただし、データセットにクラス不均衡がある場合は、正解率やマイクロ平均だけでは不十分なこともあります。マクロ平均や加重平均も併せて確認することで、より公平で実態に即した評価が可能になります。
今回は、Pythonによるロジスティック回帰(とソフトマックス回帰)の概要と仕組み、基本的なプログラミングを説明しました。知識を定着させるために、余裕があれば、末尾の実力試しもやってみてください。
次回は、分類タスクの手法として決定木を解説します。お楽しみに。
実力試しクイズ
オレンジ色の部分をクリックまたはタップすると答えが表示されます。ヒントが欲しい場合は、緑色の部分をクリックしてください。穴埋め問題に使える選択肢が表示されます。
問題
二項ロジスティック回帰は、入力データと出力結果の関係を「線形結合とロジスティック関数」によってモデル化し、0か1の二値分類を行う手法です。scikit-learnでは、LogisticRegressionクラスを使って実装できます。
ロジスティック関数は、直線をS字型の曲線に変換することで、0.0〜1.0の確率値を出力します。この値に対して0.5などの閾値(しきいち)を設定し、どちらのクラスに分類するかを判断します。グラフ上でこの境界を示す線は、決定境界と呼ばれます。
モデルのパラメーターは、交差エントロピーという損失関数を最小化するよう最尤推定によって求められ、勾配降下法などの最適化アルゴリズムが使われます。分類モデルの性能を評価する際には、正解率、適合率、再現率、F1スコアといった複数の指標が用いられます。
ソフトマックス回帰は、多クラス分類に対応した多項ロジスティック回帰の一種であり、ロジスティック関数の代わりにソフトマックス関数を使用します。基本的な仕組みは、ロジスティック回帰と共通です。
ヒント: 決定境界 直線 多クラス LogisticRegression 適合率 二値 勾配降下 線形 誤差逆伝播 交差エントロピー 尤度 LogisticClassification 分類線 N字 陽性率 実数 ソフトマックス関数 確率 シグモイド関数 S字
「機械学習入門」
Copyright© Digital Advantage Corp. All Rights Reserved.