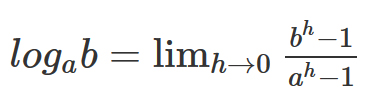機械学習の精度を左右する「データ加工」の基礎知識――「攻めのデータ加工」=「特徴量エンジニアリング」編:「AI」エンジニアになるための「基礎数学」再入門(5)(2/2 ページ)
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。前回から2回に分けて「データ加工」の手法を紹介します。今回は「攻めのデータ加工」です。
量的データの加工
量的データは基本的に数値としてデータを持っています(時々、Excelブックなどの「1,000」という形式のものは文字として読み込んでしまうこともあるので、ご注意を)。
これから紹介するテクニックは、基本的にデータの質を高めるようなものです。さらに言えば、機械学習のアルゴリズムがうまく計算できるように下ごしらえをしておくというようなイメージです。
単純化
「単純化」は、詳し過ぎる、複雑過ぎる情報をあえて単純な情報へと置き換える手法です。情報量は落ちますが、ノイズとなるような無駄な情報が落ちてくれることを期待できます。
- Rounding
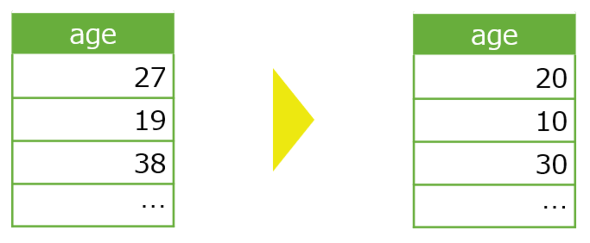
Roundingは、要するに端数処理です。数字を「丸める」や「平たくする」ともいわれています。実数の有効数字の桁数を小さくするような処理を加えます。
この例では「age」の1の位を切り捨ててやることで、10代、20代など年代を表す値に変換できています。もしも、年齢による細かな違いよりも、年代による大まかなライフスタイルや思考が予測したいことがらに関係していると考えられる場合には有効でしょう。
年齢を年代に変更する他の主なものには、何かしらの金額を四捨五入で百円単位などに変更するというものがあります。
- Binning
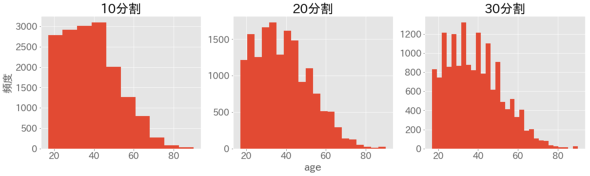
Binningの説明をする前に、まずはageのヒストグラムを見てみましょう。
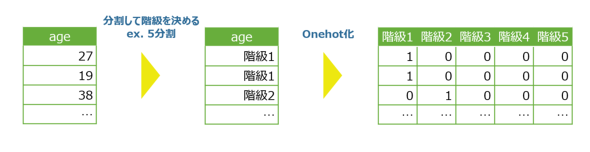
これを見ると、分割数が小さい(=階級幅が大きい)ほどデータが大まかに、つまりは情報量が少なくなっていることが分かります。Binningでは、初めに「データを何分割にするか」を決めます。後の処理は下図の通りです。
このように、Binningは量的変数をあえて質的変数へと変換することで単純化するテクニックです。こうすることで、予測したいデータとの関係性が複雑(=非線形)でも、ある程度予測することが可能になることがあります。
スケーリング(Scaling)
機械学習のアルゴリズムが量的データを扱う上では、上記の複雑性の他に、「データの平均値や標準偏差(ひっくるめてスケール)がバラバラで、どのデータが重要か比較ができず、うまく計算できない」というような問題が発生することがあります(※なお、平均や標準偏差の意味については第3回の記事をご覧ください)。
身近な例で言えば、田中さんはテストで次のような結果でした。どちらの科目の方が優秀だったといえるでしょうか。
- 数学のテストで50点
- 英語のテストで60点
一概にどちらが優秀とはいえません。なぜならば、数学は平均を越えていて、英語は平均を下回っている可能性だってあるわけです。要するに、比較する際はスケールをそろえる(=スケーリング)必要があります。
- 標準化(Standardization)
標準化は「z-score化」と呼ばれたりもします。z-scoreというのは簡単にいえばレア度のようなものです。z-scoreと珍しさの対応は大まかに次の通りです。
| z-score | 珍しさ |
|---|---|
| -2 | 下位2.5%程度(悪い意味で40人に1人) |
| -1 | 下位16%程度(悪い意味で6人に1人) |
| 0 | 普通 |
| +1 | 上位16%程度(良い意味で6人に1人) |
| +2 | 上位2.5%程度(良い意味で40人に1人) |
お気付きの方もいるかと思いますが、このz-scoreに10をかけて50を足したものが「偏差値」です。
| 偏差値 | 珍しさ |
|---|---|
| 30 | 下位2.5%程度 |
| 40 | 下位16%程度 |
| 50 | 普通 |
| 60 | 上位16%程度 |
| 70 | 上位2.5%程度 |
偏差値はz-scoreが見やすくなるようにひと手間加えただけなので、計算はz-scoreまでで十分です。ここで、先ほどの田中さんのテスト結果をz-scoreに変換するとどうでしょうか。
- 数学のテストのz-scoreが2
- 英語のテストでz-scoreが-1
明らかに数学の方が優秀であるといえます。また、こうすることで機械でも優劣を判断できるような数字へと変換できています。故にうまく計算できるというわけです。CensusDatasetでもageやcapital-gainなど幾つか数値型のデータがあるので、基本的には全て標準化しておきましょう。
それでは、z-scoreの有用さが分かったところで、その計算は次のように行います。
z-scoreはレア度と先述しましたが、つまりは「偏差が平均的な偏差(標準偏差)の幾つ分か?」という値をもって、珍しさを表現しているわけです。
Pythonでこの計算をするならば次のようになります。
# 平均を計算する関数
def mean(x):
n = len(x)
sigma = sum(x)
return sigma / n
# 分散を計算する関数
def var(x):
x_mean = mean(x)
d = [(val - x_mean)**2 for val in x] # 偏差の2乗を計算
return mean(d)
# 標準化の関数
def standardization(x):
x_mean = mean(x)
x_var = var(x)
x_std = x_var**(1/2)
zscores = [(val - x_mean)/x_std for val in x] # 偏差/標準偏差
return zscores
# ex. 4人の学生のテストの点数
test_res = [90, 75, 67, 62]
standardization(test_res)
# 結果: [1.5573662880039287, 0.14157875345490262, -0.6135079316379113, -1.08543710982092]
標準化はNumpyやPandasを使うことで、簡単に処理を記述できますが、それらのライブラリの中では上記のような計算が行われているとイメージしてください。
- 正規化(Normalization)
あまり使用する機会はありませんが、標準化とは別のスケーリング方法もあります。正規化は、主に画像データなどの前処理として行うもので、例えばRGB(0〜255の値)を0〜1の間に収めておくと、ニューラルネットワークなどで画像認識などをする際に計算負荷を抑えるような効果があります。
どのように、値を0〜1の間に収めるかというと、次の通りです。
分子の値は、小さくとも0(最小値 - 最小値)、大きくとも最大値 - 最小値なので、変換後の値(score)は必ず0〜1の間に収まるというわけです。
Pythonでこの数式を表すと次のようになります。
# 正規化の関数
def normalization(x):
x_max = max(x)
x_min = min(x)
scores = [(val - x_min)/(x_max - x_min) for val in x]
return scores
# ex. RGBのRの値
r = [0, 255, 117, 81]
normalization(r)
# 結果: [0.0, 1.0, 0.4588235294117647, 0.3176470588235294]
なお、画像データのRGBの値は基本的に0〜255の範囲の値であることが分かっているので、maxやminは計算せずに、それぞれ定数として255、0とすることの方が多いです。
変換(Transformation)
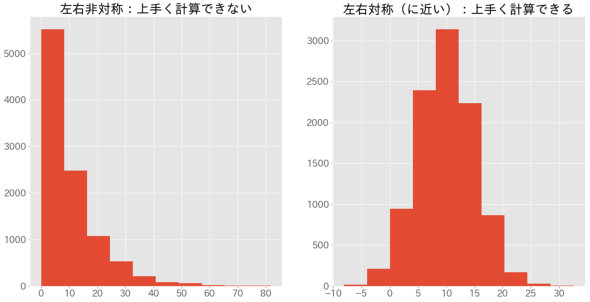
最後に紹介する量的データを扱う際の問題は、「分布(ヒストグラムの概形)がゆがんでいてうまく計算できない」というようなものです(※機械学習の範囲を学習していくと理由が分かります)。なお、「ゆがんでいる」というのは、下図のように概形が左右非対称であることを指しています。
ここで紹介する「変換」と呼ばれる手法は、こういった“ゆがみ”を補正するためのものです。
- 対数(log)変換
対数変換は最も頻繁に用いられる変換方法です。まずは、「対数とはどのようなものか?」という点をおさらいしておきましょう。
対数とは、「log底真数」で書き表されるものです。計算結果は「真数は底の何乗か」を考えた場合の「何乗」の部分を表す数値(「冪指数」と呼びます)になります。例えば、8は2の3乗(2×2×2)ですが、その8を真数、2を底とした場合には、「log28=3」となります。なじみのない方は、「logab=c」を見たら、「aを何乗するとbになりますか。それはcです」という具合に頭の中で日本語に置き換えて考えるといいでしょう。
対数の計算は、「極限」を使った式で表すと下記のようになります。
これをPythonで表現したものが下記です。ただし、「limh→0」はhに小さな値を代入することで表現しているので計算結果は正確ではありません。
def log(a, b):
"""
対数の近似計算を行う。
Parameters
----------
a : float
底
b : float
真数
"""
h = 1e-10 # hは0以上で、小さな数を入れるほど正確な計算結果が得られる。
num = b**h - 1
den = a**h - 1
return num/den
補足として、「logab=c」を、a進数でbを表現する際に必要な桁数がc+1という捉え方もできます(答えに小数点以下が含まれることがあるため、その場合はしっくりこない解釈かもしれません)。この桁数の概念を利用した対数の近似計算も紹介するので参考にしてください。
def log(a, b):
"""
対数の近似計算を行う。返す値はa進数でbを表現する場合に必要な桁数-1。
Parameters
----------
a : float
底
b : float
真数
"""
if b/a >= 1:
return 1 + log(a, b/a)
else:
return 0
なお、底が特定の数の場合は、次のように表記が省略されたり、変わったりします。真数は全て「x」としています。
| 底 | 呼称 | 表記 |
|---|---|---|
| 2 | 二進対数 | lg x |
| 10 | 常用対数 | log x |
| ネイピア数「e」 | 自然対数 | ln xあるいはlog x |
| ※「ネイピア数」とは、円周率のような特別な数字で、その値は「2.71……」です。どのような値であるかは、後の章で解説する予定です。 ※常用対数と自然対数の表記がかぶるので注意しましょう。特に断りがなければ、log xは基本的に自然対数です。 | ||
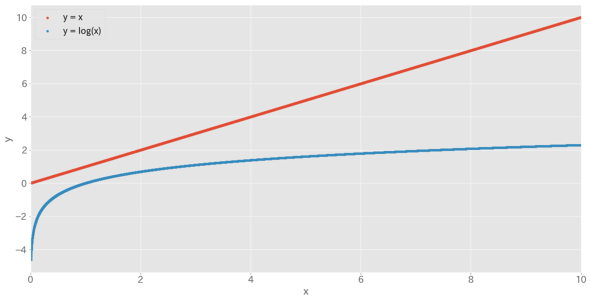
ここで、「y=x」と「y=log x 」のグラフを比較してみましょう。
グラフから分かるように、対数(自然対数)は入力xの値が大きくなればなるほど、その値の大きさを抑え込むような働きがあります。
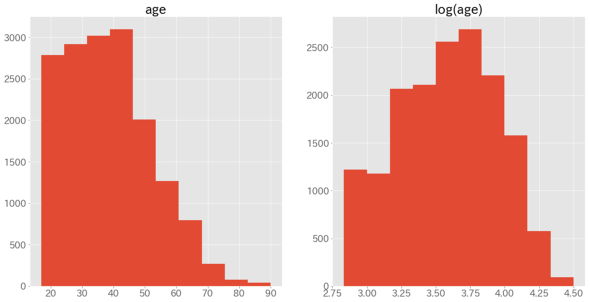
さて、この対数をデータに適用させると、どのように分布の概形が変化するでしょうか。
ageは、もともと右にゆがんだ分布でしたが、対数変換後はより左右対称に近い分布へと変わっていることが確認できました。なお、「log(0)」は計算できないため、もしデータの中に0が出現するようであれば、一律で+1してからlog()に入力することで計算が可能になります。
変換の様子が分かるように、Pythonのコードで補足しておきます。
from math import log # logを計算する関数をimport
def transform_log(x):
return [log(val) for val in x]
# ex. 年齢データ
age = [90, 46, 37, 45, 40]
transform_log(age)
# 結果: [4.499809670330265, 3.828641396489095, 3.6109179126442243, 3.8066624897703196, 3.6888794541139363]
- その他の変換
対数変換以外はあまり使用されることはありませんが、他にも平方根変換や指数変換であったり、時間を表すようなデータを三角関数で変換したりすることもあります。
次回は「集合」「数列」について
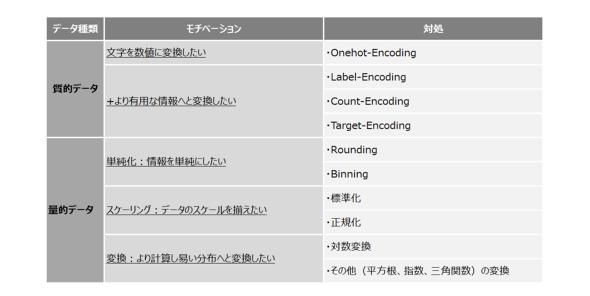
最後に、今回紹介した手法をおさらいしてみましょう。
今回紹介したテクニックについて、「なぜ施すのか?」という点で、専門用語が出現したこともあり、合点がいかないところが多々あると思います。これを解消するためには、今後解説していく「確率、確率分布」や「関数」といった基礎部分をはじめとして、「回帰」や「最小二乗法」など応用部分を学ぶ必要があります。
また、データ加工のテクニックはこの他にもたくさんあります。その全てを記憶することは難しいですし、記憶しているだけでは的確な手法選択ができません。従って、先述の基礎や応用をしっかりと理解することで、「このようなデータであれば、このように加工したら有用なのではないか?」という仮説を立てられるようになることを目指していきましょう。
次回は「集合」「数列」について解説します。それ以降の「確率、確率分布」などを理解する上でも大切な範囲になっていますので、ぜひともご覧ください。
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
 数学ができると「数学ができないエンジニアはダメだ」の効果が計れる
数学ができると「数学ができないエンジニアはダメだ」の効果が計れる
数学ができるとエンジニアとして活躍できるのか、むしろ数学ができないとエンジニア失格なのか?――「エンジニアに数学の知識は必要か?」を、数学オタクが論理的に解説します。![[Python入門]Pythonってどんな言語なの?](https://image.itmedia.co.jp/ait/articles/1904/02/news024.gif) [Python入門]Pythonってどんな言語なの?
[Python入門]Pythonってどんな言語なの?
機械学習に取り組んでみたいという人に(そうでない人にも)向けて、Pythonプログラミングを基礎からやさしく解説する連載をPython 3.10に合わせて改訂します。 Pythonで機械学習/Deep Learningを始めるなら知っておきたいライブラリ/ツール7選
Pythonで機械学習/Deep Learningを始めるなら知っておきたいライブラリ/ツール7選
最近流行の機械学習/Deep Learningを試してみたいという人のために、Pythonを使った機械学習について主要なライブラリ/ツールの使い方を中心に解説する連載。初回は、筆者が実業務で有用としているライブラリ/ツールを7つ紹介します。