IT投資効果の算出法は本当に役に立つのか?:システム部門Q&A(4)
情報マネージャの頭を悩ませているのが、ITの効果測定法だ。現在、ROI法やDCF法などさまざまな計算方法が存在するが、これらからどのようなことが明らかになるのか。また、こうした計算方法はどの程度“使える”のか。
質問
情報化投資の費用対効果を計算する方法として、DCF法とかROI法など多くの手法がありますが、どのような違いがあるのでしょうか? また、実際にこのような方法で情報化投資の評価ができるのでしょうか?
投資の採算計算では、「NPV法」「DCF法」「IRR法」「ROI法」などいろいろな名称の方法がありますが、どれも同じような原理に基づいています。なお、これらは情報化投資だけでなく、店舗や生産設備など一般的な投資を対象にしたものですが、ここでは情報化投資を対象とします。
採算計算の原理:概念はむしろ簡単だ
投資をしてから廃棄するまでのキャッシュフローを図示すると図のようになります。当初(0年目)に初期投資を行うことにより、毎年その維持のための費用(キャッシュフローの減少:赤の部分)を掛けることにより収入(キャッシュフローの増大:黄の部分)が得られますので、その差が毎年の名目的な利益(キャッシュフローの純増:青の部分)になります。
ところが、現在100万円を得るのと、1年後に100万円を得るのとでは価値が違います。その割引率を10%とするならば、1年後の100万円の現在価値は、100/(1+0.1)=約91万円に相当します。同様に2年後の100万円は100/(1+0.1)2=約83万円に相当します。そのような処理を「現在価値に変換する」といいますが、図で青の部分を現在価値に変換したものが緑の部分になります。
この緑の部分の合計が初期投資と比較して大きければこの投資は有利であり、小さければ不利であるというのが採算計算の原理です。
ここで、初期投資を「C」、j年後の名目的な利益を「Aj」、割引率を「i」とすると、割引後の値Pは次の式で表されます。
P=−C+A1/(1+i)+A2/(1+i)2+・・・+Aj/(1+i)j+・・・+An/(1+i)n
注:この式にn年後の残存価値も考慮にいれる必要がありますが、以下の議論に本質的な影響はないので省略します
採算計算方法の種類:すべて同じようなものだ
先に挙げた各種の方法は、この式を多様な観点で表現したものです。一般的には次のような区分になりますが、人によって異なることもあります。
(1)ROI(Return On Investment:投下資本利益率)法
ROI法とは、広義には投資に対してどれだけの効果があるかを計算する方法であり、すべての投資の採算計算といえますが、会計的な利益・損失ではなくキャッシュフローの増減をベースにして計算すること、割引率として資本利益率を用いることなどに限定した計算方法を指します。なお、ここで紹介する方法は、すべてキャッシュフローをベースにしています。
(2)DCF(Discount Cash Flow)法
毎年のキャッシュフローを現在価値に変換して初期投資と比較すること、すなわち、上の式で評価する方法をDCF(Discount Cash Flow)法といいます。
ほとんどの企業では、すでに乾いたぞうきんを絞るような合理化努力が重ねられてきました。残っている問題は、「Aを解決しようとすればBに副作用が生じる。Bを防ぐにはCの対処が必要だが、Cを重視するとAと逆な事態になる」というような、複雑な問題です。これに対処するには、全体をシステムとしてとらえ、個々のサブシステム間の関係、上位のシステムとの関係を正確に認識する「システム思考」が求められます。
(3)NPV(Net Present Value:正味現在価値)法
DCF法のうち、割引率iの値を与えてPの正負により評価する方法をNPV(Net Present Value:正味現在価値)法といいます。NPV法は現在価値で評価しますが、毎年どれだけの利益になるかを尺度にする場合もあり、それを年価法といいます。
(4)IRR(Internal Rate of Return:内部収益率)法
それに対して、P=0になるような割引率iを計算により求め、その値の大きいものを採用するとか、ある基準値よりも大きければ採用するという方法をIRR(Internal Rate of Return:内部収益率)法といいます。このiの値あるいは基準値のことを内部収益率といいます。なお、IRR法のことをDCF法ということもあります。ROI法を狭義にとらえれば、このiを資本利益率としたものだともいえます。
(5)回収年法
また、上の式を左から計算していき、P≧0になるnを求めて、nが小さければ採用する方法を回収年法といいます(そのnを回収年という)。しかし、これは短期間に費用を回収できるかというリスクの観点の尺度であり、採算性の尺度とするのは不適切です。
採算計算の限界:現実には使えない
すでにお気付きのように、これらの方法で採算性を評価するには、初期投資、毎年のキャッシュフロー、使用期間(方法によっては割引率も)が与件になります。それらについて信頼度の高い値が得られるならばこの方法は効果的です。しかし、現実の情報化投資では困難なのではないでしょうか?
初期投資の測定は比較的容易ですが、それでも「222の法則」(第2回「なぜ情報化投資は初期計画より増えるのか?」参照)により、2倍程度の予算超過は覚悟しておく必要があります。
毎年の費用では、TCO論議のようにパソコン1台の維持費用は、当初の取得費用の数倍だといわれていますし、効果の面では、例えばペーパーレスを目的とするシステムでの紙1枚を減らすことによる効果は、次のように1円から1000円までの違いが生じます。
- 紙の価格(大した費用ではありません)
- プリンタやキャビネットなどの費用、設置床面積費用
- 印刷、コピー、配布の人件費、検索のための人件費、消耗品在庫管理の費用
- 検索が面倒だという理由で、参照あるいは再利用されないことによる逸失利益(かなりの額になるでしょう)
まして、戦略的な情報システムの場合には、毎年のキャッシュフローを測定すること自体が戦略策定を左右することになります。
さらに重要なことは、先に示した計算式で最も影響が大きいのは対象年数nです。nが大きければほとんどの場合はP>0になるでしょうが、nが小さければP<0になるのは当然です。それなのに、計画している情報システムの寿命は経営環境や情報技術発展に直接に影響されます。すなわち誰にもnの値は分からないのです。
このように不確定要素が大きいときには、上の式が役にたたないのは自明です。不確定要素をカバーするために、上の式の値をいろいろ変化させて統計化確率的な検討をすることもできましょうし、最近流行の金融工学を応用することもできましょうが、Ajが数倍どころか数十倍の誤差があり、nが不明だとしたら、どうしようもありません。逆にいえば、これらの値が精度よく与えられるのであれば、このような計算をするまでもなく、直感的にPの正負は判断できるでしょう。
採算計算の効果:真の目的を成熟度向上に
情報システム、特に戦略的要素の高い情報システムの採算性が、上記のような計算式を用いて判断できるというのは幻想にすぎません。しかし、このような考え方を導入することにより、投資に関する成熟度を向上させることができるのです。そして、それは単に該当投資の評価だけではなく、業務改善や改革に役立つインフラ整備にもなるのです。
(1)定性的効果の金銭価値:精度ではなく正確度を
採算計算をするためには、上述の「紙1枚の費用」で指摘した効果を明確にする必要があります。波及効果のどこまでを考慮に入れるかの合意を得ることであり、そのときの値は50円なのか300円なのかというオーダーレベルでの評価であり、「購入価格が1円ではなく1円23銭である」というような精度を追求するのは無意味です。さらにいえば、当初から事実を追究するのではなく、最初は「この程度だとしておこう」という合意で設定しておき、逐次いろいろな検討により事実に近づけていけばよいのです。
1人・時の省力化効果、伝票ミス1件の費用、BtoCサイトへの顧客アクセス1件の効果など、多くの要因についてこのような換算値が作成され、必要に応じて更新されているならば、個々の投資案件ごとに算出する必要はありませんし、何を重点に改善・改革すればよいかの資料になります。
(2)検討論理の合理化:関係者の共通認識
投資検討時に森羅万象を検討することはできません。できるだけ少ない対象に絞り込む必要があります。また、その効果や費用を把握するのにどの金銭価値尺度を用いたかを明確にすることが必要です。その過程により関係者の合意ができれば、半自動的に採算性の合意ができます。合意が得られない場合でも、いくつかのケースに限定されますので、どの場合にはPの値やiの値がどうなるかを計算することは簡単ですし、どの要因についてもっと厳密に検討すればよいかが明確になります。
(3)モニタリング項目の明確化
計画時に採算性が良いと判断されても、開発過程や実施後に計画時と異なる状況になるのは当然です。それを早期に発見して解決することが重要ですが、「2」での検討を行うことにより、何をモニタリング指標として監視すればよいのかが、比較的明確になります。予期しない事態が発生することもありますが、それは今後の投資での検討項目に加えることにより成熟度が向上します。
この記事に対するご意見をお寄せください [email protected]
筆者プロフィール
木暮 仁(こぐれ ひとし)
東京生まれ。東京工業大学卒業。コスモ石油、コスモコンピュータセンター、東京経営短期大学教授を経て、現在フリー。情報関連資格は技術士(情報工学)、中小企業診断士、ITコーディネータ、システム監査、ISMS審査員補など。経営と情報の関係につき、経営側・提供側・利用側からタテマエとホンネの双方からの検討に興味を持ち、執筆、講演、大学非常勤講師などをしている。著書は「教科書 情報と社会」「情報システム部門再入門」(ともに日科技連出版社)など多数。http://www.kogures.com/hitoshi/にて、大学での授業テキストや講演の内容などを公開している
関連記事
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
人気記事ランキング
- Excelの外部リンク無効化へ Microsoftがセキュリティ強化に向けた新方針
- BIOSに隠れて常駐する高度な新型マルウェア「Shade BIOS」の脅威
- 富士通とNECの最新受注状況から探る「国内IT需要の行方」
- 今後不満続出? オンライン証券の不正アクセスへの金銭補償で「損」しないには
- Z世代を狙う新たな脅威 副業ブームに忍び寄るサイバー攻撃
- OpenAI「gpt-oss」発表 “o4-mini級”の性能をオープンに
- 「セキュリティ後回しで生成AI導入」の末路 アクセンチュアが警告
- 「リストアしたら中身が○○?」 ランサムウェア暗号化で起きた“怖い話”
- 推論強化版Gemini「Deep Think」リリース 数学五輪メダリスト級モデルの威力
- 「私はロボットではありません」をAIが突破? 使われたプロンプトとは
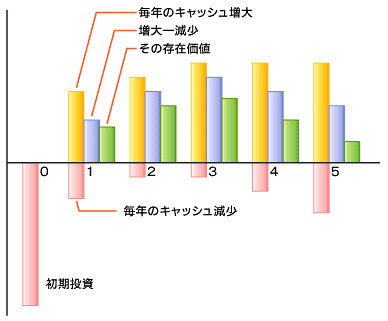 図 投資から廃棄までのキャッシュフロー
図 投資から廃棄までのキャッシュフロー